
���� ��1��������a=$\sqrt{3}$����b=1��c=2���������Ҷ������cosC=$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2ab}$=0���ɵ�sinC��ֵ��
��2���������������Ҷ������A��ֵ����S��ABC=3$\sqrt{3}$���bc=12��������GΪ��ABC�����ģ��ٽ��AMΪBC���ϵ����ߣ����������Լ����Ҷ�������������ʽ���AM����Сֵ���ɴ����AG����Сֵ�Լ���ʱb��ֵ��
��� �⣺��1���������������Ҷ����ɵã�����֮��Ϊa��b��c=$\sqrt{3}$��1��2��
������a=$\sqrt{3}$����b=1��c=2������cosC=$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2ab}$=0���ɵ�C=$\frac{��}{2}$����sinC=1��
��2����c2+c2+bc=a2����cosA=$\frac{{b}^{2}{+c}^{2}{-a}^{2}}{2bc}$=-$\frac{1}{2}$����A=$\frac{2��}{3}$��
����AM��BC�߳������ߣ�G��AM�ϵĵ㣬��$\overrightarrow{AG}$=2$\overrightarrow{GM}$���ɵ�GΪ��ABC�����ģ�
S��ABC=3$\sqrt{3}$=$\frac{1}{2}$bc•sinA=$\frac{\sqrt{3}}{4}$bc����bc=12��
��${��2\overrightarrow{AM}��}^{2}$=${��\overrightarrow{AB}+\overrightarrow{AC}��}^{2}$=c2+b2-2bc•cosA��2bc+bc=3bc=36��
��AM��3�����ҽ���b=c=2$\sqrt{3}$ʱ���Ⱥų�����
��AM����СֵΪ$\sqrt{3}$��AG����СֵΪ$\frac{2}{3}$AM=2����ʱb=2$\sqrt{3}$��
���� ������Ҫ�������Ҷ��������Ҷ�����Ӧ�ã���������ʽ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
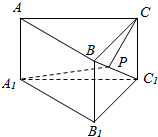 ��ֱ������ABC-A1B1C1�У�����Ϊֱ�����ǡ�ACB=90�㣬AC=$\sqrt{2}$��BC=CC1=1��P��BC1��һ���㣬��A1P+PC����Сֵ��$\sqrt{5}$��
��ֱ������ABC-A1B1C1�У�����Ϊֱ�����ǡ�ACB=90�㣬AC=$\sqrt{2}$��BC=CC1=1��P��BC1��һ���㣬��A1P+PC����Сֵ��$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCDΪ���Σ�AD��ƽ��ABE��AE=EB=BC=2��FΪCE�ϵĵ㣬��BF��ƽ��ACE��
��ͼ���ı���ABCDΪ���Σ�AD��ƽ��ABE��AE=EB=BC=2��FΪCE�ϵĵ㣬��BF��ƽ��ACE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1��2��4} | B�� | {0��3��5} | C�� | {0��1��3��4��5} | D�� | ∅ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com