
分析 (1)由题意,得Sn+1?Sn=Sn+1-Sn,两边同时除以 Sn+1?Sn 得$1=\frac{1}{{S}_{n}}-\frac{1}{{S}_{n+1}}$,即可证明结论;
(2)写出Sn,即可求an.
解答 (1)证明:由Sn+1?Sn=an+1 及an+1=Sn+1-Sn,得Sn+1?Sn=Sn+1-Sn(n∈N+),
若存在 Sn=0,则 an=Sn?Sn-1=0,从而 Sn-1=Sn-an=0.
以此类推知 S1=0,矛盾,故Sn≠0(n∈N+).
从而两边同时除以 Sn+1?Sn 得$1=\frac{1}{{S}_{n}}-\frac{1}{{S}_{n+1}}$,即$\frac{1}{{S}_{n+1}}-\frac{1}{{S}_{n}}=-1(n∈{N}_{+})$,
所以 $\left\{\frac{1}{{S}_{n}}\right\}$ 是首项为 $\frac{9}{2}$,公差为-1 的等差数列.
(2)解:由(1)知,$\frac{1}{{S}_{n}}=\frac{9}{2}-(n-1)=\frac{11}{2}-n$,
故${S}_{n}=\frac{2}{11-2n}(n∈{N}_{+})$.
从而n≥2,an=Sn-Sn-1=$\frac{4}{(11-2n)(13-2n)}$,
n=1,a1=$\frac{2}{9}$,
所以${a}_{n}=\left\{\begin{array}{l}\frac{2}{9},&n=1\\ \frac{4}{(11-2n)(13-2n)},&n≥2.\end{array}\right.$.
点评 本题考查等差数列的证明,考查数列的通项与求和,考查学生的计算能力,属于中档题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{5}}{3}$ | B. | -$\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{17}{4}$ | C. | $-\frac{29}{5}$ | D. | $2-\frac{{9\sqrt{7}}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
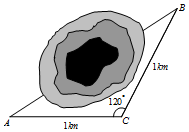 如图,在高速公路建设中需要确定隧道的长度,工程技术人员已测得隧道两端的两点A、B到点C的距离AC=BC=1km,且∠ACB=120°,则A、B两点间的距离为( )
如图,在高速公路建设中需要确定隧道的长度,工程技术人员已测得隧道两端的两点A、B到点C的距离AC=BC=1km,且∠ACB=120°,则A、B两点间的距离为( )| A. | $\sqrt{3}$km | B. | $\sqrt{2}$km | C. | 1.5km | D. | 2km |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com