
【题目】如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为![]() 的圆弧,则该几何体的体积是( )
的圆弧,则该几何体的体积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】如图,网格纸上小正方形的边长为![]() ,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数y=f(x)满足f(﹣2)=f(4)=﹣16,且f(x)最大值为2.
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)在[t,t+1](t>0)上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记全集U={1,2,3,4,5,6,7,8},A={1,2,3,5},B={2,4,6},则图中阴影部分所表示的集合是( ) 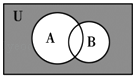
A.{4,6,7,8}
B.{2}
C.{7,8}
D.{1,2,3,4,5,6}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=log2x,x∈(0,2),若关于x的方程|g(x)|2+m|g(x)|+2m+3=0有三个不同实数解,则实数m的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知偶函数f(x)的定义域为R,且在(﹣∞,0)上是增函数,则f(﹣ ![]() )与f(a2﹣a+1)(a∈R)的大小关系是( )
)与f(a2﹣a+1)(a∈R)的大小关系是( )
A.f(﹣ ![]() )≤f(a2﹣a+1)
)≤f(a2﹣a+1)
B.f(﹣ ![]() )≥f(a2﹣a+1)?
)≥f(a2﹣a+1)?
C.f(﹣ ![]() )<f(a2﹣a+1)
)<f(a2﹣a+1)
D.f(﹣ ![]() )>f(a2﹣a+1)
)>f(a2﹣a+1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com