
����Ŀ����ͼ���ı���ABCD��ABEF��Ϊ���Σ�BC=BE=2AB�������E��AB��C�Ĵ�СΪ ![]() ���ֽ���ACD����AC��תһ�ܣ�������ת�����У��� ��
���ֽ���ACD����AC��תһ�ܣ�������ת�����У��� �� 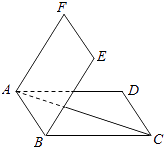
A.������ij��λ�ã�ʹ��ֱ��AD��BE���ɵĽ�Ϊ ![]()
B.����ij��λ�ã�ʹ��ֱ��AD��BE���ɵĽ�Ϊ ![]()
C.������ij��λ�ã�ʹ��ֱ��AD��ƽ��ABEF���ɵĽ�Ϊ ![]()
D.����ij��λ�ã�ʹ��ֱ��AD��ƽ��ABEF���ɵĽ�Ϊ ![]()
 ��ǰ����ϵ�д�
��ǰ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=ln��x+m����mx��
������f��x���ĵ������䣻
������m��1��x1 �� x2Ϊ����f��x����������㣬��֤��x1+x2��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��y2=2x�Ľ���ΪF��ƽ����x�������ֱ��l1 �� l2�ֱ�C��A��B���㣬��C������P��Q���㣮
��1����F���߶�AB�ϣ�R��PQ���е㣬֤��AR��FQ��
��2������PQF������ǡ�ABF���������������AB�е�Ĺ켣���̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AB=AD=CD=1��BD= ![]() ��BD��CD�����ı���ABCD�ضԽ���BD�۳�������A�䩁BCD��ʹƽ��A��BD��ƽ��BCD�������н�����ȷ���ǣ� ��
��BD��CD�����ı���ABCD�ضԽ���BD�۳�������A�䩁BCD��ʹƽ��A��BD��ƽ��BCD�������н�����ȷ���ǣ� �� 
A.A��C��BD
B.��BA��C=90��
C.CA����ƽ��A��BD���ɵĽ�Ϊ30��
D.������A�䩁BCD�����Ϊ ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�PC��ƽ��ABCD��AB��DC��DC��AC��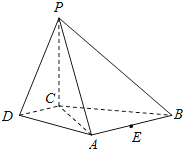
��1����֤��DC��ƽ��PAC��
��2����֤��ƽ��PAB��ƽ��PAC��
��3�����EΪAB���е㣬����PB���Ƿ���ڵ�F��ʹ��PA��ƽ��CEF��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��λ���� ![]() ��
�� ![]() �ļн�Ϊ
�ļн�Ϊ ![]() ��������
�������� ![]() =x
=x ![]() +y
+y ![]() ��x��y��R����|
��x��y��R����| ![]() ��
�� ![]() ��
�� ![]() |=1����x+2y�����ֵΪ ��
|=1����x+2y�����ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����60m���ĸֲģ�Ҫ������ͼ��ʾ�Ĵ��� 
��1�������y�봰���x�ĺ�����ϵ��
��2���������Ϊ������ʱ�����y�����ֵ�����ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C���Եı߷ֱ���a��b��c����a=2��2cos2 ![]() +sinA=
+sinA= ![]() ��
��
��1�������������ġ�ABC����ֻ��һ������b��ȡֵ��Χ��
��2������ABC���ܳ�ȡ���ֵʱ����b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������{an}��ǰn���ΪSn �� ��a ![]() +2an=4Sn��n��N*����
+2an=4Sn��n��N*����
��1����an��
��2��������{bn}���㣺b1=1��bn= ![]() ��n��N* �� n��2����������{bn}��ǰn���Tn ��
��n��N* �� n��2����������{bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com