
【题目】已知抛物线![]() 的准线与半椭圆
的准线与半椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若点![]() 是半椭圆
是半椭圆![]() 上一动点,过点
上一动点,过点![]() 作抛物线
作抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)由抛物线准线与椭圆相交的弦长构建方程求得p值即可;
(Ⅱ)设点![]() 坐标为
坐标为![]() ,由题意可知切线斜率不会为0,设出两条切线的直线方程,联立直线与抛物线方程,由相切关系构建方程,并由两切点分别得到
,由题意可知切线斜率不会为0,设出两条切线的直线方程,联立直线与抛物线方程,由相切关系构建方程,并由两切点分别得到![]() 是方程
是方程![]() 的两根,进而由韦达定理与直线和方程的关系可知
的两根,进而由韦达定理与直线和方程的关系可知![]() ,
,![]() 是
是![]() 的两点,再由点到直线的距离公式和弦长公式表示
的两点,再由点到直线的距离公式和弦长公式表示![]() 的底和高从而表示面积,最后换元求函数的最值即可.
的底和高从而表示面积,最后换元求函数的最值即可.
(Ⅰ)由题可知,抛物线![]() 的准线为
的准线为![]() ,则有
,则有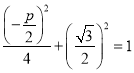 得
得![]() ,
,
所以![]() .
.
(Ⅱ)设点![]() 坐标为
坐标为![]() ,且满足
,且满足![]() .
.
由题意可知切线斜率不会为0,即设切线![]() 为
为![]() ,
,
代入![]() 得
得![]() ,
,
由![]() 可得
可得![]() ①,
①,
设切点![]() ,抛物线的上半部曲线函数关系式为
,抛物线的上半部曲线函数关系式为![]() ,则
,则![]() ,
,
故![]() ,将其代入①可得
,将其代入①可得![]() ②.
②.
设切线![]() 为
为![]() ,切点
,切点![]() ,同理可得
,同理可得![]() ③.
③.
由②③可知![]() 是方程
是方程![]() 的两根,所以
的两根,所以![]() ,
,![]() ,
,
又![]() ,
,![]() ,所以代入②③可知
,所以代入②③可知![]() ,
,![]() 是
是![]() 的两点,即
的两点,即![]() 直线方程为
直线方程为![]() .
.
故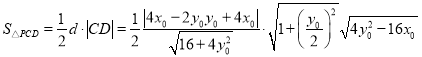

又因为![]() 且
且![]() ,所以
,所以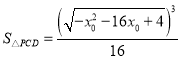 .
.
令![]() ,由二次函数性质可知,其在
,由二次函数性质可知,其在![]() 上单调递减,故
上单调递减,故![]() ,
,
所以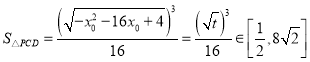


科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 是曲线
是曲线![]() 上的一个动眯,当
上的一个动眯,当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离的最小值;
的距离的最小值;
(2)若曲线![]() 上所有的点都在直线
上所有的点都在直线![]() 的右下方,求实数
的右下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2022年北京冬奥运动会即第24届冬季奥林匹克运动会将在2022年2月4日至2月20日在北京和张家口举行,某研究机构为了了解大学生对冰壶运动的兴趣,随机从某大学生中抽取了100人进行调查,经统计男生与女生的人数比为![]() ,男生中有20人表示对冰壶运动有兴趣,女生中有15人对冰壶运动没有兴趣.
,男生中有20人表示对冰壶运动有兴趣,女生中有15人对冰壶运动没有兴趣.
(1)完成![]() 列联表,并判断能否有
列联表,并判断能否有![]() 把握认为“对冰壶运动是否有兴趣与性别有关”?
把握认为“对冰壶运动是否有兴趣与性别有关”?
有兴趣 | 没有兴趣 | 合计 | |
男 | 20 | ||
女 | 15 | ||
合计 | 100 |
(2)用分层抽样的方法从样本中对冰壶运动有兴趣的学生中抽取6人,求抽取的男生和女生分别为多少人?若从这6人中选取两人作为冰壶运动的宣传员,求选取的2人中恰好有1位男生和1位女生的概率.
附: ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年5月17日晚“2019年感动中国人物名单揭晓”,中国女排位列其中,在感动中国的舞台上,她们的一句“我们没赢够”,再次鼓舞中国人民中国之光——中国女排,一次次在逆境中绝地反击,赢得奥运冠军,“女排精神”也是我们当前处于“新冠”逆境中的高三学子们学习的榜样,前进的动力.一次比赛中,中国女排能够闯入决赛的概率为0.8,在闯入决赛条件下中国女排能够获胜的概率是0.9,则中国女排闯进决赛且获得冠军的概率是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元前5世纪,古希腊哲学家芝诺发表了著名的阿基里斯悖论:他提出让乌龟在跑步英雄阿基里斯前面1000米处开始与阿基里斯赛跑,并且假定阿基里斯的速度是乌龟的10倍.当比赛开始后,若阿基里斯跑了1000米,此时乌龟便领先他100米,当阿基里斯跑完下一个100米时,乌龟领先他10米,当阿基里斯跑完下一个10米时,乌龟先他1米....所以,阿基里斯永远追不上乌龟.按照这样的规律,若阿基里斯和乌龟的距离恰好为0.001米时,乌龟爬行的总距离为( )
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】辽宁省六校协作体(葫芦岛第一高中、东港二中、凤城一中、北镇高中、瓦房店高中、丹东四中)中的某校文科实验班的![]() 名学生期中考试的语文、数学成绩都不低于
名学生期中考试的语文、数学成绩都不低于![]() 分,其中语文成绩的频率分布直方图如图所示,成绩分组区间是:
分,其中语文成绩的频率分布直方图如图所示,成绩分组区间是:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
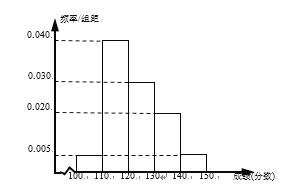
(1)根据频率分布直方图,估计这![]() 名学生语文成绩的中位数和平均数;(同一组数据用该区间的中点值作代表;中位数精确到
名学生语文成绩的中位数和平均数;(同一组数据用该区间的中点值作代表;中位数精确到![]() )
)
(2)若这![]() 名学生语文成绩某些分数段的人数
名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示:
之比如下表所示:
分组区间 |
|
|
|
|
|
|
|
|
|
从数学成绩在![]() 的学生中随机选取
的学生中随机选取![]() 人,求选出的
人,求选出的![]() 人中恰好有
人中恰好有![]() 人数学成绩在
人数学成绩在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com