
【题目】以下四个命题:
①对立事件一定是互斥事件;
②函数y=x+ ![]() 的最小值为2;
的最小值为2;
③八位二进制数能表示的最大十进制数为256;
④在△ABC中,若a=80,b=150,A=30°,则该三角形有两解.
其中正确命题的个数为( )
A.4
B.3
C.2
D.1
【答案】C
【解析】解:对于①,由互斥事件和对立事件的概念知,对立事件一定是互斥事件,
互斥事件不一定是对立事件,①正确;
对于②,当x>0时,函数y=x+ ![]() 的最小值为2,
的最小值为2,
当x<0时,函数y=x+ ![]() 的最大值为﹣2,∴②错误;
的最大值为﹣2,∴②错误;
对于③,八位二进制数能表示的最大十进制数是
1×20+1×21+1×22+…+1×27= ![]() =255,③错误;
=255,③错误;
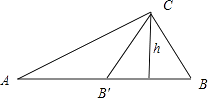
对于④,如图所示,△ABC中,a=80,b=150,A=30°,
∴C到AB的距离h=bsinA=75,由h<a<b,
得该三角形有两解,④正确.
综上,正确的命题为①④.
所以答案是:C.
【考点精析】通过灵活运用命题的真假判断与应用,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数 ![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c且acosB=4,bsinA=3.
(1)求tanB及边长a的值;
(2)若△ABC的面积S=9,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知2sinA﹣cosB=2sinBcosC,且角B为钝角.
(1)求角C的大小;
(2)若a=2,b2+c2﹣a2= ![]() bc,求△ABC的面积.
bc,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,MCN是某海湾旅游区的一角,为营造更加优美的旅游环境,旅游区管委会决定建立面积为4 ![]() 平方千米的三角形主题游戏乐园ABC,并在区域CDE建立水上餐厅.已知∠ACB=120°,∠DCE=30°.
平方千米的三角形主题游戏乐园ABC,并在区域CDE建立水上餐厅.已知∠ACB=120°,∠DCE=30°.
(1)设AC=x,AB=y,用x表示y,并求y的最小值;
(2)设∠ACD=θ(θ为锐角),当AB最小时,用θ表示区域CDE的面积S,并求S的最小值.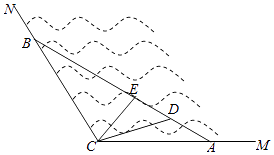
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +ax,x>1.
+ax,x>1.
(1)若函数f(x)在 ![]() 处取得极值,求a的值;
处取得极值,求a的值;
(2)若方程(2x﹣m)lnx+x=0在(1,e]上有两个不等实根,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com