
【题目】如图,已知椭圆C:![]() +y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.
+y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.
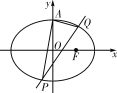
(1)求椭圆C的方程;
(2)若不过点A的动直线l与椭圆C相交于P,Q两点,且![]() =0,求证:直线l过定点,并求出该定点N的坐标.
=0,求证:直线l过定点,并求出该定点N的坐标.
【答案】(1)![]() +y2=1(2)证明见解析,定点N
+y2=1(2)证明见解析,定点N![]() .
.
【解析】
(1)利用直线AF与圆相切可求得a(圆心到直线的距离等于半径),从而得椭圆方程;
(2)由![]() =0,知AP⊥AQ,从而直线AP与坐标轴不垂直,设直线AP的方程为y=kx+1,代入椭圆方程可求得P点坐标,同理可得Q点坐标,写出直线PQ方程,化简后可知其所过定点.
=0,知AP⊥AQ,从而直线AP与坐标轴不垂直,设直线AP的方程为y=kx+1,代入椭圆方程可求得P点坐标,同理可得Q点坐标,写出直线PQ方程,化简后可知其所过定点.
(1)将圆M的一般方程x2+y2-6x-2y+7=0化为标准方程为(x-3)2+(y-1)2=3,圆M的圆心为M(3,1),半径为r=![]() .
.
由A(0,1),F(c,0)(c=![]() )得直线AF:
)得直线AF:![]() +y=1,即x+cy-c=0.
+y=1,即x+cy-c=0.
由直线AF与圆M相切得![]() =
=![]() .
.
所以c=![]() 或c=-
或c=-![]() (舍去).所以a=
(舍去).所以a=![]() ,
,
所以椭圆C的方程为![]() +y2=1.
+y2=1.
(2)证明:由![]() =0,知AP⊥AQ,从而直线AP与坐标轴不垂直,
=0,知AP⊥AQ,从而直线AP与坐标轴不垂直,
由A(0,1)可设直线AP的方程为y=kx+1,直线AQ的方程为y=-![]() x+1(k≠0),
x+1(k≠0),
将y=kx+1代入椭圆C的方程![]() +y2=1并整理,得(1+3k2)x2+6kx=0,
+y2=1并整理,得(1+3k2)x2+6kx=0,
解得x=0或x=-![]() ,
,
因此P的坐标为 ,即
,即 .
.
将上式中的k换成-![]() ,得Q
,得Q .
.
所以直线l的方程为y= ·
·![]() +
+![]() ,
,
化简得直线l的方程为y=![]() x-
x-![]() .
.
因此直线l过定点N![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.

(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求二面角A1-BC1-B1的余弦值;
(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图是正方体的平面展开图.在这个正方体中,
①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.
以上四个命题中,正确命题的序号是________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln(x+1)+x2+1,g(x)=﹣x2﹣2mx+4.
(1)当a>0时,求曲线y=f(x)的切线斜率的取值范围;
(2)当a=﹣4时,若存在x1∈[0,1],x2∈[1,2],满足f(x1)≥g(x2),求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.若函数![]() 在
在![]() 上有零点,则一定有
上有零点,则一定有![]()
B.函数![]() 既不是奇函数也不是偶函数
既不是奇函数也不是偶函数
C.若函数![]() 的值域为
的值域为![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]()
D.若函数![]() 满足条件
满足条件![]() ,
,![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB//DC,![]() ,PA
,PA![]() 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=![]() AB=1,M是PB的中点.
AB=1,M是PB的中点.
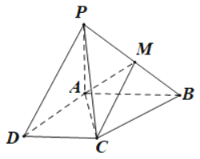
(1)证明:面PAD![]() 面PCD;
面PCD;
(2)求AC与PB所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益P与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益Q与投入
,乙城市收益Q与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com