Question

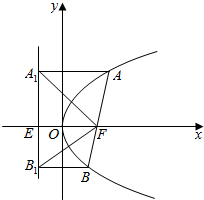
7．如图所示，线段AB时抛物线的焦点弦，F为抛物线焦点，若A，B在其准线上的射影分别为A₁，B₁，则∠A₁FB₁等于（　　）

• A． 45°
• B． 60°
• C． 90°
• D． 120°

Answer 1

分析 由抛物线的定义及内错角相等，可得∠AFA₁=∠A₁FK，同理可证∠BFB₁=∠B₁FK，由∠AFA₁+∠A₁FK+∠BFB₁+∠B₁FK=180°，可得答案．

解答 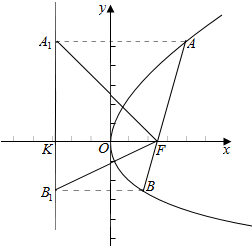解：如图：设准线与x轴的交点为K，
∵A、B在抛物线的准线上的射影为A₁、B₁，
由抛物线的定义可得，AA₁=AF，
∴∠AA₁F=∠AFA₁，
又由内错角相等得∠AA₁F=∠A₁FK，
∴∠AFA₁=∠A₁FK．
同理可证∠BFB₁=∠B₁ FK．   
由∠AFA₁+∠A₁FK+∠BFB₁+∠B₁FK=180°，
∴∠A₁FK+∠B₁FK=∠A₁FB₁=90°，
故选：C．

点评 本题考查抛物线的定义、以及简单性质的应用，推出∠AFA₁=∠A₁FK是解题的关键．