
【题目】2017年存节期间,某服装超市举办了一次有奖促销活动,消费每超过600 元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种. 方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸到2个红球,则打6折;若摸到1个红球,则打7折;若没摸到红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了 600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算.
【答案】
(1)解:选择方案一,若享受到免单优惠,则需要摸出3个红球,
设顾客享受到免单优惠为事件A,则
![]() ,
,
所以两位顾客均享受到免单的概率为
![]() ;
;
(2)解:若选择方案一,设付款金额为X元,则
X可能的取值为0,600,700,1000;
计算 ![]() ,
,
![]() ,
,
故X的分布列为:
X | 0 | 600 | 700 | 1000 |
【解析】(1)选择方案一,利用积事件的概率公式计算两位顾客均享受到免单的概率值;(2)选择方案一,计算所付款金额X的分布列和数学期望值,
选择方案二,计算所付款金额Z的数学期望值,比较得出结论.
P | | | | |
所以 ![]() (元);
(元);
若选择方案二,设摸到红球的个数为Y,付款金额为Z元,则Z=1000﹣200Y,
由已知可得 ![]() ,故
,故 ![]() ,
,
所以E(Z)=E(1000﹣200Y)=1000﹣200E(Y)=820(元),
因为E(X)<E(Z),所以该顾客选择第一种抽奖方案更合算.


科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,一个焦点F(﹣2,0),且长轴长与短轴长的比是 ![]() .
.
(1)求椭圆C的方程;
(2)设点M(m,0)在椭圆C的长轴上,点P是椭圆上任意一点.当 ![]() 最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成,AD⊥AF,AE=AD=2. (Ⅰ)证明:平面PAD⊥平面ABFE;
(Ⅱ)求正四棱锥P﹣ABCD的高h,使得二面角C﹣AF﹣P的余弦值是 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+ ![]() )﹣cos2x.
)﹣cos2x.
(1)求f(x)的最小正周期及x∈[ ![]() ,
, ![]() ]时f(x)的值域;
]时f(x)的值域;
(2)在△ABC中,角A、B、C所对的边为a,b,c,且角C为锐角,S△ABC= ![]() ,c=2,f(C+
,c=2,f(C+ ![]() )=
)= ![]() ﹣
﹣ ![]() .求a,b的值.
.求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
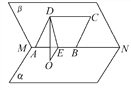
【题目】如图,已知二面角α-MN-β的大小为60°,菱形ABCD在平面β内,A,B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥平面α,垂足为O.
(1)证明:AB⊥平面ODE.
(2)求异面直线BC与OD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() ,g(x)=2x+a,若x1∈[
,g(x)=2x+a,若x1∈[ ![]() ,3],x2∈[2,3],使得f(x1)≥g(x2),则实数a的取值范围是( )
,3],x2∈[2,3],使得f(x1)≥g(x2),则实数a的取值范围是( )
A.a≤1
B.a≥1
C.a≤0
D.a≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线过点P![]() 且与x轴、y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在这样的直线满足下列条件:①△AOB的周长为12;②△AOB的面积为6.若存在,求出方程;若不存在,请说明理由.
且与x轴、y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在这样的直线满足下列条件:①△AOB的周长为12;②△AOB的面积为6.若存在,求出方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大衍数列,来源于中国古代著作《乾坤谱》中对易传“大衍之数五十”的推论.其前10项为:0、2、4、8、12、18、24、32、40、50.通项公式: 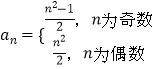 ,如果把这个数列{an}排成如图形状,并记A(m,n)表示第m行中从左向右第n个数,则A(10,4)的值为( )
,如果把这个数列{an}排成如图形状,并记A(m,n)表示第m行中从左向右第n个数,则A(10,4)的值为( ) 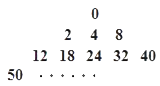
A.1200
B.1280
C.3528
D.3612
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com