
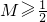 ;
;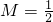 时,试求出f(x)的解析式.
时,试求出f(x)的解析式.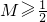
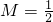 时,
时,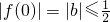 ,
,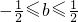 ①同理
①同理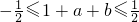 ②
②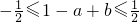 ③
③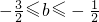 ④由①、④得:
④由①、④得: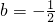 .
.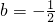 时,分别代入②、③得:
时,分别代入②、③得: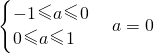 ,因此
,因此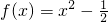 .
.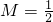 时,可得出,
时,可得出,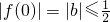 ,
,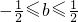 ①同理
①同理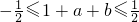 ②
②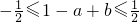 ③由这几个不等式解出a,b,c的取值范围,判断出它们的值,即可求出函数的解析式
③由这几个不等式解出a,b,c的取值范围,判断出它们的值,即可求出函数的解析式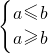 等价得出a=b,这是利用不等式求值的基础,本题考查了转化的思想,
等价得出a=b,这是利用不等式求值的基础,本题考查了转化的思想, 

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
| an |
| 3n |
| a |
| an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn; ,求数列{cn}的变号数.
,求数列{cn}的变号数.查看答案和解析>>
科目:高中数学 来源:2008-2009学年湖北省武汉市教科院高三(上)第一次调考数学试卷(文理合卷)(解析版) 题型:解答题
 ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn; ,求数列{cn}的变号数.
,求数列{cn}的变号数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com