函数
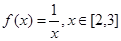
的最大值为
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
若非零函数

对任意实数
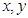
均有
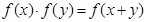
,且当
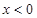
时
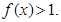
(1)求证:
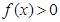
;
(2)求证:

为R上的减函数;
(3)当
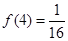
时, 对
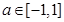
恒有
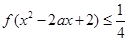
,求实数
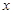
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知奇函数
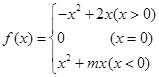
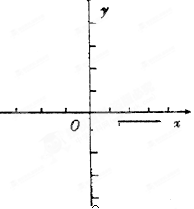
(1)求实数
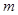
的值,并在给出的直角坐标系中画出
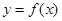
的图象;
(2)若函数
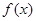
在区间
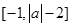
上单调递增,试确定实数
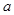
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设函数
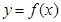
的定义域为
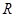
,并且满足
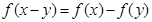
,且
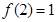
,当
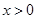
时,
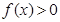
(1).求
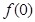
的值;(3分)
(2).判断函数
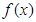
的奇偶性;(3分)
(3).如果
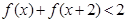
,求
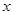
的取值范围.(6分)
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
某超市中秋前
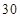
天月饼销售总量
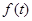
与时间
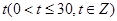
的关系大致满足
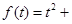
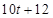
,则该超市前
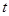
天平均售出(如前
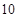
天的平均售出为
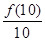
)的月饼最少为____________.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若函数
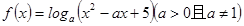
满足对任意的
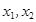
,当
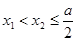
时
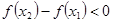
,则实数
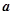
的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知函数
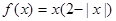
,则函数
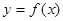
的增区间是
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知
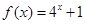
,
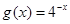
,若偶函数
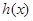
满足
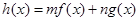
(其中m,n为常数),且最小值为1,则
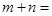
.
查看答案和解析>>
