
若非零函数 对任意实数
对任意实数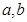 均有
均有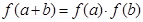 ,且当
,且当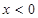 时,
时,  ;
;
(1)求证: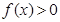 (2)求证:
(2)求证: 为减函数
为减函数
(3)当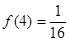 时,解不等式
时,解不等式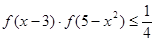
(1)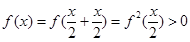 ;
;
(2)见解析;(3)不等式的解集为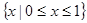 。
。
解析试题分析:(1)利用已知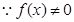
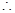
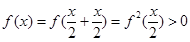 ,可得结论。
,可得结论。
(2)根据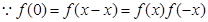 =1,得到f(x)与f(-x)的关系式,进而求解得到。
=1,得到f(x)与f(-x)的关系式,进而求解得到。
(3)由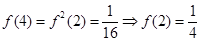 原不等式转化为
原不等式转化为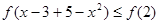 进而结合单调性得到。
进而结合单调性得到。
解:(1)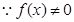
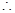
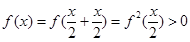 ------------3分
------------3分
(2)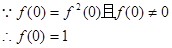 -------------5分
-------------5分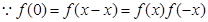
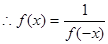 -------------8分
-------------8分
设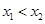 则
则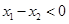
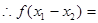
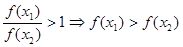 ,
, 为减函数
为减函数
-------10分
(3)由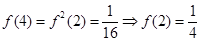 原不等式转化为
原不等式转化为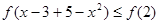 ,结合(2)得:
,结合(2)得: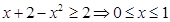
故不等式的解集为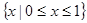 ------------------13分
------------------13分
考点:本题主要考查了函数的性质以及不等式的求解的运用。
点评:解决该试题的关键是抽象函数的赋值法思想的运用,判定单调性和f(x)与f(-x)的关系式的运用。


科目:高中数学 来源: 题型:解答题
小王需不定期地在某超市购买同一品种的大米.现有甲、乙两种不同的采购策略,策略甲:每次购买大米的数量一定;策略乙:每次购买大米的钱数一定.若以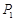 (元)和
(元)和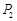 (元)分别记小王先后两次买米时,该品种大米的单价,请问:仅这两次买米而言,甲、乙两种购买方式,从平均单价考虑,哪种比较合算?请进行探讨,并给出探讨过程.
(元)分别记小王先后两次买米时,该品种大米的单价,请问:仅这两次买米而言,甲、乙两种购买方式,从平均单价考虑,哪种比较合算?请进行探讨,并给出探讨过程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某工厂修建一个长方体无盖蓄水池,其容积为4800立方米,深度为3米.池底每平方米的 造价为150元,池壁每平方米的造价为120元.设池底长方形长为 米.
米.
(1)求底面积,并用含 的表达式表示池壁面积;
的表达式表示池壁面积;
(2)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
设函数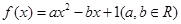 ,
,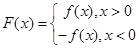
(1) 如果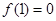 且对任意实数
且对任意实数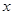 均有
均有 ,求
,求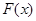 的解析式;
的解析式;
(2) 在(1)在条件下, 若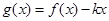 在区间
在区间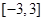 是单调函数,求实数
是单调函数,求实数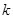 的取值范围;
的取值范围;
(3) 已知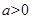 且
且 为偶函数,如果
为偶函数,如果 ,求证:
,求证: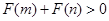 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com