
【题目】已知f(x)=lgx+1(1≤x≤100),则g(x)=f2(x)+f(x2)的值域为( )
A.[﹣2,7]
B.[2,7]
C.[﹣2,14]
D.[2,14]
【答案】B
【解析】解:由题意得, ![]() ,解得1≤x≤10,
,解得1≤x≤10,
∵f(x)=lgx+1(1≤x≤100),
∴g(x)=f2(x)+f(x2)=(lgx+1)2+1+2lgx
=(lgx)2+4lgx+2,1≤x≤10
设t=lgx,则0≤t≤1,
所以h(t)=t2+4t+2,0≤t≤1
∵h(t)在[0,1]为增函数,且h(0)=2,h(1)=7
∴h(t)=t2+4t+2(0≤t≤1)值域为[2,7],
即g(x)=f2(x)+f(x2)的值域为[2,7],
故选B.
【考点精析】根据题目的已知条件,利用函数的值域的相关知识可以得到问题的答案,需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 焦点
焦点![]() 且倾斜角的
且倾斜角的![]() 直线
直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]()
![]() 的面积为
的面积为![]() .
.
(I)求抛物线![]() 的方程;
的方程;
(II)设![]() 是直线
是直线![]() 上的一个动点,过
上的一个动点,过![]() 作抛物线
作抛物线![]() 的切线,切点分别为
的切线,切点分别为![]() 直线
直线![]() 与直线
与直线![]() 轴的交点分别为
轴的交点分别为![]() 点
点![]() 是以
是以![]() 为圆心
为圆心![]() 为半径的圆上任意两点,求
为半径的圆上任意两点,求![]() 最大时点
最大时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,左顶点为
,左顶点为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条相互垂直的直线分别与椭圆
作两条相互垂直的直线分别与椭圆![]() 交于(不同于点
交于(不同于点![]() 的)
的)![]() 两点.试判断直线
两点.试判断直线![]() 与
与![]() 轴的交点是否为定点,若是,求出定点坐标;若不是,请说明理由.
轴的交点是否为定点,若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2|x|﹣1.
(1)证明函数f(x)是偶函数;
(2)在如图所示的平面直角坐标系中作出函数f(x)的图象.并根据图象写出函数f(x)的单调区间; 
(3)求函数f(x)当x∈[﹣2,4]时的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年某市街头开始兴起“mobike”、“ofo”等共享单车,这样的共享单车为很多市民解决了最后一公里的出行难题.然而,这种模式也遇到了一些让人尴尬的问题,比如乱停乱放,或将共享单车占为“私有”等.为此,某机构就是否支持发展共享单车随机调查了50人,他们年龄的分布及支持发展共享单车的人数统计如下表:
年龄 |
|
|
|
|
|
|
受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
支持发展共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系:
列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系:
年龄低于35岁 | 年龄不低于35岁 | 合计 | |
支持 | |||
不支持 | |||
合计 |
(Ⅱ)若对年龄在![]() 的被调查人中随机选取两人,对年龄在
的被调查人中随机选取两人,对年龄在![]() 的被调查人中随机选取一人进行调查,求选中的3人中支持发展共享单车的人数为2人的概率.
的被调查人中随机选取一人进行调查,求选中的3人中支持发展共享单车的人数为2人的概率.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: 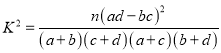 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=![]() AE=2,O,M分别为CE,AB的中点.
AE=2,O,M分别为CE,AB的中点.
(1)求证:OD∥平面ABC;
(2)求直线CD和平面ODM所成角的正弦值;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,数列{an}满足a1=1,an+1=f(an)(n∈N*).
,数列{an}满足a1=1,an+1=f(an)(n∈N*).
(1)证明数列{![]() }是等差数列,并求出数列{an}的通项公式;
}是等差数列,并求出数列{an}的通项公式;
(2)记Sn=a1a2+a2a3+…+anan+1,求Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com