Question

已知抛物线的顶点在原点,焦点在x轴的正半轴上,抛物线上的点M(3,m)到焦点的距离等于5,求抛物线的方程和m的值.

Answer 1

分析:解本题的基本思路有两个:其一设抛物线方程,利用点M在抛物线上和点M到焦点的距离等于5,列出关于m、p的方程组,解关于m、p的方程组;其二利用抛物线的定义,得点M到准线的距离为5,直接得p的关系式,求出p值.

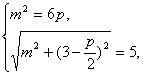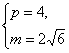解法一:设抛物线方程为y²=2px(p＞0),则焦点F(,0),由题设可得解之得或

故所求的抛物线方程为y²=8x,m的值为±2.

解法二:设抛物线方程为y²=2px(p＞0),焦点F(,0),准线方程x=-,根据抛物线定义,点M到焦点的距离等于M到准线的距离,则3+=5,∴p=4.

因此抛物线方程为y²=8x.

又点M(3,m)在抛物线上,于是m²=24.∴m=±26.

点评:涉及抛物线上一点与焦点的距离问题要注意利用定义转化为到准线的距离,可简化计算.