
分析 (1)由函数的解析式可得sin(x+$\frac{π}{2}$)≠0,可得 x+$\frac{π}{2}$≠kπ,k∈z,由此求得x的范围,可得函数的定义域.
(2)由条件利用同角三角函数的基本关系、二倍角公式求得sin2α和cos2α的值,再利用两角差的余弦公式求得f(α)的值.
解答 解:(1)对于函数f(x)=$\frac{{1+\sqrt{2}cos(2x-\frac{π}{4})}}{{sin(x+\frac{π}{2})}}$,显然,sin(x+$\frac{π}{2}$)≠0,∴x+$\frac{π}{2}$≠kπ,k∈z,
求得x≠kπ-$\frac{π}{2}$,k∈z,故函数的定义域为[x|x≠kπ-$\frac{π}{2}$,k∈z }.
(2)∵角α是第四象限角,且cosα=$\frac{3}{5}$,∴sinα=-$\frac{4}{5}$,∴sin2α=2sinαcosα=-$\frac{24}{25}$,cos2α=2cos2α-1=-$\frac{7}{25}$,
则 f(α)=$\frac{1+\sqrt{2}cos(2α-\frac{π}{4})}{sin(α+\frac{π}{2})}$=$\frac{1+\sqrt{2}(\frac{\sqrt{2}}{2}cos2α+\frac{\sqrt{2}}{2}sin2α)}{cosα}$=$\frac{1+cos2α+sin2α}{cosα}$=$\frac{1-\frac{7}{25}-\frac{24}{25}}{\frac{3}{5}}$=-$\frac{2}{5}$.
点评 本题主要考查利用诱导公式进行化简求值,同角三角函数的基本关系、两角差的余弦公式,属于基础题.


科目:高中数学 来源: 题型:解答题
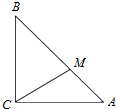 如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,
如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第9项 | B. | 第8项 | C. | 第9项和第10项 | D. | 第8项和第9项 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\sqrt{3}$ | C. | 1 | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
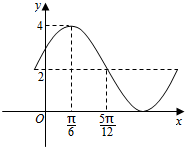 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则其解析式为y=2sin(2x+$\frac{π}{6}$)+2..
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则其解析式为y=2sin(2x+$\frac{π}{6}$)+2..查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com