
【题目】2017年交警统计了某路段过往车辆的车速大小与发生交通事故的次数,得到如表所示的数据:
车速x(km/h) | 60 | 70 | 80 | 90 | 100 |
事故次数y | 1 | 3 | 6 | 9 | 11 |
(1)请画出上表数据的散点图;

(2)请根据上表提供的数据,求出y关于x的线性回归方程![]() =
=![]() x+
x+![]() ;
;
(3)根据(2)所得速度与事故发生次数的规律,试说明交管部门可采取什么措施以减少事故的发生.
附:![]() =
=![]() ,
,![]() =
=![]() -
-![]()
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2x-x2)ex-1.
(1)求函数f(x)的单调区间;
(2)若对任意x≥1,都有f(x)-mx-1+m≤0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是两条不同直线,
是两条不同直线,![]() ,
,![]() 是两个不同平面,则下列命题正确的是 ( )
是两个不同平面,则下列命题正确的是 ( )
A. 若![]() ,
,![]() 垂直于同一平面,则
垂直于同一平面,则![]() 与
与![]() 平行
平行
B. 若![]() ,则
,则![]()
C. 若![]() ,
,![]() 不平行,则在
不平行,则在![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
D. 若![]() ,
,![]() 不平行,则
不平行,则![]() 与
与![]() 不可能垂直于同一平面
不可能垂直于同一平面
查看答案和解析>>
科目:高中数学 来源: 题型:
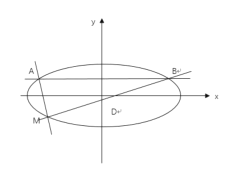
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,左焦点
,左焦点![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点, ![]() 为椭圆上异于
为椭圆上异于![]() 的点.
的点.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 过
过![]() 点,求圆
点,求圆![]() 的标准方程;
的标准方程;
(3)设直线![]() 与
与![]() 轴分别交于
轴分别交于![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,得到如图的频率分布直方图(图1).

(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到图2中数据,根据表中的数据,能否在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com