
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
分析 由两角和的正弦把三角函数化简,结合已知求出周期,进一步得到ω,则三角函数的解析式可求,再由图象平移得到g(x)的解析式,确定满足g(x)≥1的范围,根据几何概型利用长度之比可得结论.
解答 解:f(x)=$\sqrt{3}$sinωx+cosωx=2sin(ωx+$\frac{π}{6}$),
∵f(x)=$\sqrt{3}$sinωx+cosωx(ω>0)的图象与x轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,
∴函数f(x)的周期T=2×$\frac{π}{2}$=π,
即$\frac{2π}{ω}$=π,则ω=2,
即f(x)=2sin(2x+$\frac{π}{6}$),
把函数f(x)的图象沿x轴向右平移$\frac{π}{6}$个单位,
得g(x)=f(x-$\frac{π}{6}$)=2sin[2(x-$\frac{π}{6}$)+$\frac{π}{6}$]=2sin(2x-$\frac{π}{6}$).
由2sin(2x-$\frac{π}{6}$)≥1,x∈[0,π],可得sin(2x-$\frac{π}{6}$)$≥\frac{1}{2}$,
由2kπ+$\frac{π}{6}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{5π}{6}$,k∈Z,
得kπ+$\frac{π}{6}$≤x≤kπ+$\frac{π}{2}$,k∈Z,
∵x∈[0,π],
∴当k=0时,解得:x∈[$\frac{π}{6}$,$\frac{π}{2}$],
∴事件“g(x)≥1”发生的概率为$\frac{\frac{π}{2}-\frac{π}{6}}{π}$=$\frac{\frac{π}{3}}{π}$=$\frac{1}{3}$.
故选:B.
点评 本题考查了几何概型的概率的计算,考查了三角函数的图象和性质,本题考查几何概型,三角函数的化简,学生的计算能力,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
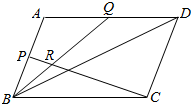 如图所示,?ABCD中,P点在线段AB上,且$\frac{AP}{PB}$=m,Q在线段AD上,且$\frac{AQ}{QD}$=n,BQ与CP相交于点R,求$\frac{PR}{RC}$的值.
如图所示,?ABCD中,P点在线段AB上,且$\frac{AP}{PB}$=m,Q在线段AD上,且$\frac{AQ}{QD}$=n,BQ与CP相交于点R,求$\frac{PR}{RC}$的值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{π}{3}$ | B. | $-\frac{π}{6}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com