Question

【题目】已知抛物线x2=2py上点（2，2）处的切线经过椭圆 的两个顶点．
（1）求椭圆E的方程；
（2）过椭圆E的上顶点A的两条斜率之积为﹣4的直线与该椭圆交于B，C两点，是否存在一点D，使得直线BC恒过该点？若存在，请求出定点D的坐标；若不存在，请说明理由；
（3）在（2）的条件下，若△ABC的重心为G，当边BC的端点在椭圆E上运动时，求|GA|2+|GB|2+|GC|2的取值范围．

Answer 1

【答案】
（1）解：把（2，2）代入抛物线方程x2=2py，得22=2p×2，解得p=1，

∴抛物线的方程为x2=2y；

∴y′=x，∴抛物线x2=2y在点（2，2）处的切线的斜率为y′|x=2=2，

∴抛物线在点（2，2）处的切线方程为y﹣2=2（x﹣2），化为y=2x﹣2．

它与两坐标轴的交点分别为（1，0），（0，﹣2），由题意可得a=2，b=1．

∴椭圆的方程为

（2）解：假设直线BC恒过定点D，由题意可知直线BC的斜率必存在，故可设直线BC的方程为y=kx+m（m≠2）．

设B（x1，y1），C（x2，y2）．由（1）知A（0，2）．

联立 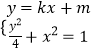消去y得到（k2+4）x2+2kmx+m2﹣4=0，

由△＞0，得（2km）2﹣4（k2+4）（m2﹣4）＞0，化为k2﹣m2+4＞0．

∴ ，

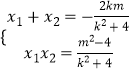∴kABkAC=

=

=

=

=

= = ．

由题意可得 ，解得m=0，满足△＞0．

∴直线BC的方程为y=kx，直线BC恒过定点D（0，0）

（3）解：由（2）可知：原点（0，0）在直线BC上，

由椭圆的对称性可知AO为△ABC的边BC上的中线，由|AG|=2|GO|和A（0，2），得G点的坐标为 ．

∴ ．

∴|GA|2+|GB|2+|GC|2= + = = = ．

不妨设点C在y轴的右侧，则x2∈（0，1]．

∴ ，即求|GA|2+|GB|2+|GC|2的取值范围是

【解析】（1）把（2，2）代入抛物线方程x2=2py，即可得到p，即可得到抛物线的方程．利用导数即可得到切线的斜率，利用点斜式即可得到切线方程，即可求出与坐标轴的交点坐标，即可得到a，b．可得椭圆的方程．（2）假设直线BC恒过定点D，由题意可知直线BC的斜率必存在，故可设直线BC的方程为y=kx+m（m≠2）．
设（x1 ， y1），C（x2 ， y2）．由（1）知A（0，2）．把直线方程与椭圆方程联立可得△＞0及根与系数的关系，再利用kABkAC= 即可得出m．进而可得答案．（3）利用椭圆的性质和三角形的重心性质即可得出．