
| A. | (1) | B. | (1)(2) | C. | (1)(2)(4) | D. | (1)(3)(4) |
分析 根据两个函数的定义域相同,对应关系也相同,即可判断它们是同一函数.
解答 解:对于(1),函数y=x2+|x|+2=x2-x+2,x≤0,与函数y=x2-x+2,x≤0的定义域相同,对应关系也相同,是同一函数;
对于(2),函数y=t2-t+2,t≤0,与函数y=x2-x+2,x≤0的定义域相同,对应关系也相同,是同一函数;
对于(3),函数y=x2-|x|+2=x2-x+2,x≥0,与函数y=x2-x+2,x≤0的定义域不同,不是同一函数;
对于(4),函数y=${(\sqrt{-x})}^{2}$+$\sqrt{{x}^{4}}$+2=x2-x+2,x≤0,与函数y=x2-x+2,x≤0的定义域相同,对应关系也相同,是同一函数.
所以与函数y=x2-x+2,x≤0相等的有(1)(2)(4).
故选:C.
点评 本题考查了判断两个函数是否为同一函数的应用问题,是基础题目.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:解答题
 如图一块长方形区域ABCD,AD=2,AB=1,在边AD的中点O处有一个可转动
如图一块长方形区域ABCD,AD=2,AB=1,在边AD的中点O处有一个可转动查看答案和解析>>
科目:高中数学 来源: 题型:解答题
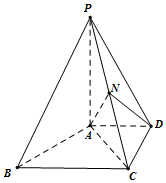 如图,在四棱锥P-ABCD中,PA⊥面ABCD,PA=BC=4,AD=2,AC=AB=3,AD∥BC,N是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,PA=BC=4,AD=2,AC=AB=3,AD∥BC,N是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2017 | B. | -2016 | C. | 2016 | D. | 2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 函数f(x)的图象如图所示,曲线BCD为抛物线的一部分.
函数f(x)的图象如图所示,曲线BCD为抛物线的一部分.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
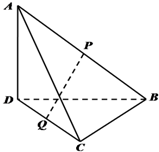 如图,在四面体ABCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,P,Q分别是线段AB与CD的中点.
如图,在四面体ABCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,P,Q分别是线段AB与CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com