
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2017届江西鹰潭一中高三上学期期中数学(理)试卷(解析版) 题型:填空题
在钝角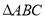 中,
中,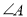 为钝角,令
为钝角,令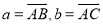 ,若
,若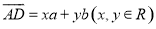 .现给出下面结论:
.现给出下面结论:
①当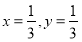 时,点
时,点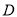 是
是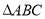 的重心;
的重心;
②记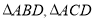 的面积分别为
的面积分别为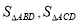 ,当
,当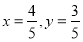 时,
时,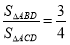 ;
;
③若点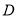 在
在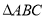 内部(不含边界),则
内部(不含边界),则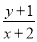 的取值范围是
的取值范围是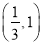 ;
;
④若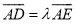 ,其中点
,其中点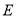 在直线
在直线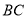 上,则当
上,则当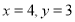 时,
时,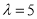 .
.
其中正确的有______________(写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西右玉一中高二上期中数学试卷(解析版) 题型:解答题
已知圆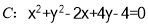 ,问是否存在斜率为1的直线
,问是否存在斜率为1的直线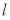 ,使
,使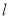 被圆
被圆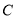 截得弦
截得弦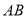 ,且以
,且以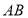 为直径的圆经过原点
为直径的圆经过原点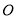 ?若存在,求出直线
?若存在,求出直线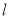 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西右玉一中高二上期中数学试卷(解析版) 题型:选择题
设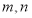 是两条不同的直线,
是两条不同的直线,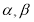 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )
①若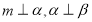 ,则
,则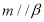 ;
;
②若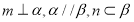 ,则
,则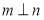 ;
;
③若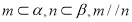 ,则
,则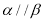 ;
;
④若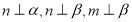 ,则
,则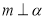 .
.
A.①② B.③④
C.①③ D.②④
查看答案和解析>>
科目:高中数学 来源:2017届福建福州外国语学校高三理适应性考试三数学试卷(解析版) 题型:解答题
已知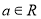 ,函数
,函数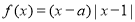 .
.
(1)若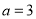 ,求
,求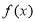 的单调递增区间;
的单调递增区间;
(2)函数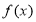 在
在 上的值域为
上的值域为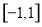 ,求
,求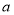 ,
,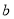 需要满足的条件.
需要满足的条件.
查看答案和解析>>
科目:高中数学 来源:2017届福建福州外国语学校高三理适应性考试三数学试卷(解析版) 题型:选择题
我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数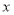 的不足近似值和过剩近似值分别为
的不足近似值和过剩近似值分别为 和
和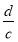 (
(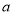 ,
,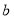 ,
,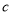 ,
,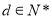 ),则
),则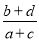 是
是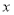 的更为精确的不足近似值或过剩近似值.我们知道
的更为精确的不足近似值或过剩近似值.我们知道 …,若令
…,若令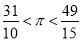 ,则第一次用“调日法”后得
,则第一次用“调日法”后得 是
是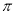 的更为精确的过剩近似值,即
的更为精确的过剩近似值,即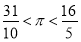 ,若每次都取最简分数,那么第四次用“调日法”后可得
,若每次都取最简分数,那么第四次用“调日法”后可得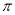 的近似分数为( )
的近似分数为( )
A.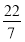 B.
B.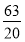 C.
C.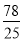 D.
D.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东广州执信中学高一上学期期中数学试卷(解析版) 题型:选择题
定义在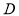 上的函数
上的函数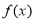 若同时满足:①存在
若同时满足:①存在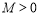 ,使得对任意的
,使得对任意的 ,都有
,都有 ;②
;② 的图像存在对称中心.则称
的图像存在对称中心.则称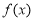 为“
为“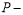 函数”.已知函数
函数”.已知函数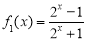 和
和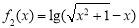 ,则以下结论一定正确的是( )
,则以下结论一定正确的是( )
A. 和
和  都是
都是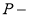 函数
函数
B. 是
是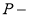 函数,
函数, 不是
不是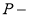 函数
函数
C. 不是
不是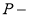 函数,
函数, 是
是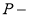 函数
函数
D. 和
和  都不是
都不是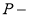 函数
函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com