
已知函数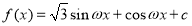 (
(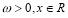 ,
,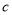 是实数常数)的图像上的一个最高点
是实数常数)的图像上的一个最高点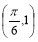 ,与该最高点最近的一个最低点是
,与该最高点最近的一个最低点是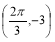 ,
,
(1)求函数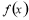 的解析式及其单调增区间;
的解析式及其单调增区间;
(2)在锐角三角形△ABC中,角A、B、C所对的边分别为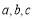 ,且
,且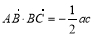 ,角A的取值范围是区间M,当
,角A的取值范围是区间M,当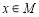 时,试求函数
时,试求函数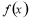 的取值范围.
的取值范围.
(1)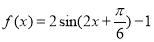 ,单调递增区间是
,单调递增区间是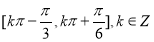 ;(2)
;(2)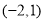 .
.
【解析】
试题分析:
(1)本题考查五点法作函数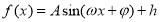 的图象,最高点到最低点之间横坐标之差为半个周期,函数式可先化简为
的图象,最高点到最低点之间横坐标之差为半个周期,函数式可先化简为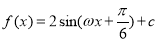 ,再根据其性质,可列出关于
,再根据其性质,可列出关于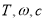 的方程,得出结论;(2)利用向量数量积的定义,可求得
的方程,得出结论;(2)利用向量数量积的定义,可求得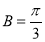 ,这时要注意向量
,这时要注意向量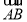 与
与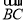 的夹角是
的夹角是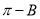 ,不是
,不是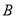 ,再利用锐角三角形的定义可求出
,再利用锐角三角形的定义可求出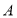 的取值范围,即
的取值范围,即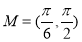 ,此时只要求得
,此时只要求得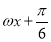 的范围,就可借助于正弦函数的性质求得
的范围,就可借助于正弦函数的性质求得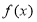 的取值范围.
的取值范围.
(1)∵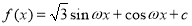 ,
,
∴ .
.
∵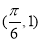 和
和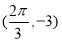 分别是函数图像上相邻的最高点和最低点,
分别是函数图像上相邻的最高点和最低点,
∴ 解得
解得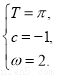
∴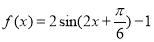 .
.
由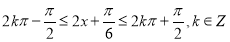 ,解得
,解得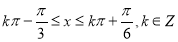 .
.
∴函数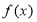 的单调递增区间是
的单调递增区间是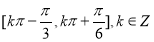 .
.
(2)∵在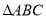 中,
中,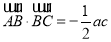 ,
,
∴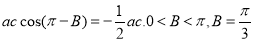 .
.
∴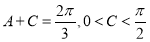 ,即
,即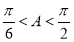 .
.
∴ .
.
当 时,
时, ,考察正弦函数
,考察正弦函数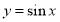 的图像,可知,
的图像,可知,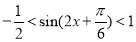 .
.
∴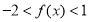 ,即函数
,即函数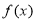 的取值范围是
的取值范围是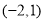 .
.
考点:(1)五点法作函数 的图象;(2)数量积,三角函数的值域.
的图象;(2)数量积,三角函数的值域.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测三数学试卷(解析版) 题型:解答题
已知实数 ,函数
,函数 。
。
(1)当 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)若 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)若当 时,函数
时,函数 图象上的点均在不等式
图象上的点均在不等式 ,所表示的平面区域内,求实数
,所表示的平面区域内,求实数 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测三数学试卷(解析版) 题型:填空题
抽样统计甲,乙两个城市连续5天的空气质量指数(AQI),数据如下:
城市 | 空气质量指数(AQI) | ||||
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | |
甲 | 109 | 111 | 132 | 118 | 110 |
乙 | 110 | 111 | 115 | 132 | 112 |
则空气质量指数(AQI)较为稳定(方差较小)的城市为 (填甲或乙).
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三下学期4月周练理科数学试卷(解析版) 题型:填空题
若中心在原点、焦点在坐标轴上的双曲线的一条渐近线方程为 ,则此双曲线的离心率为
,则此双曲线的离心率为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com