练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角性”．

    该表由若干行数字组成，从第二行起，每一行中的数字均等于其“肩上”两数之和，表中最后一行仅有一个数，则这个数为（ ）
    A.2017×22015
    B.2017×22014
    C.2016×22015
    D.2016×22014

    【答案】B
    【解析】解：由题意，数表的每一行都是等差数列，
    且第一行公差为1，第二行公差为2，第三行公差为4，…，第2015行公差为22014 ，
    故第1行的第一个数为：2×2﹣1 ，
    第2行的第一个数为：3×20 ，
    第3行的第一个数为：4×21 ，
    …
    第n行的第一个数为：（n+1）×2n﹣2 ，
    第2016行只有M，
    则M=（1+2016）22014=2017×22014
    故选：B．
    【考点精析】关于本题考查的归纳推理，需要了解根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图1，在△中， ， ， 分别为边的中点，点分别为线段的中点．将△沿折起到△的位置，使．点为线段上的一点，如图2．

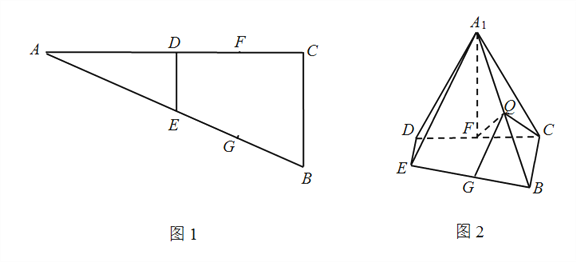
    （Ⅰ）求证： ；

    （Ⅱ）线段上是否存在点使得平面？若存在，求出的长，若不存在，请说明理由；

    （Ⅲ）当时，求直线与平面所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设全集为实数集R，A={x|3≤x＜7}，B={x| ≤2x≤8}，C={x|x＜a}．
    （1）求R（A∪B）
    （2）如果A∩C≠，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两位小学生各有2008年奥运吉祥物“福娃”5个（其中“贝贝”、“晶晶”、“欢欢”、“迎迎”和“妮妮各一个”），现以投掷一个骰子的方式进行游戏，规则如下：当出现向上的点数是奇数时，甲赢得乙一个福娃；否则乙赢得甲一个福娃，规定掷骰子的次数达9次时，或在此前某人已赢得所有福娃时游戏终止．记游戏终止时投掷骰子的次数为ξ
    （1）求掷骰子的次数为7的概率；
    （2）求ξ的分布列及数学期望Eξ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某研究小组到社区了解参加健美操运动人员的情况，用分层抽样的方法抽取了40人进行调查，按照年龄分成五个小组： ，并绘制成如图所示的频率分布直方图.

    （1）求该社区参加健美操运动人员的平均年龄；

    （2）如果研究小组从该样本中年龄在和的6人中随机地抽取出2人进行深入采访，求被采访的2人，年龄恰好都在内的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场举行有奖促销活动，顾客购买一定金额商品后即可抽奖，每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中，各随机摸出1个球，在摸出的2个球中，若都是红球，则获一等奖，若只有1个红球，则获二等奖；若没有红球，则不获奖．
    （1）求顾客抽奖1次能获奖的概率；
    （2）若某顾客有3次抽奖机会，记该顾客在3次抽奖中获一等奖的次数为X，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益函数为R（x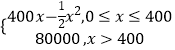）= ，其中x是仪器的产量（单位：台）；
    （1）将利润f（x）表示为产量x的函数（利润=总收益﹣总成本）；
    （2）当产量x为多少台时，公司所获利润最大？最大利润是多少元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【选修4-4：坐标系与参数方程】

    在直角坐标系中圆C的参数方程为（为参数），以原点O为极点， 轴的非负半轴为极轴建立极坐标系，直线的极坐标方程为

    （1）求圆C的直角坐标方程及其圆心C的直角坐标；

    （2）设直线与曲线交于两点，求的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）图象的一部分如图所示，函数g（x）=f（x+ ），则下列结论正确的是（ ）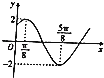

    A.函数g（x）的奇函数
    B.函数f（x）与g（x）的图象均关于直线x=﹣ π对称
    C.函数f（x）与g（x）的图象均关于点（﹣ ，0）对称
    D.函数f（x）与g（x）在区间（﹣ ，0）上均单调递增

    查看答案和解析>>

    同步练习册答案