
分析 (1)根据诱导公式和$tanα=\frac{sinα}{cosα}$化简即可;
(2)根据$tanα=\frac{sinα}{cosα}$、两角差的正弦公式、二倍角的正弦公式、诱导公式化简即可.
解答 解:(1)原式=$\frac{-tana•cosa•(-cosa)}{-cosα•sina}$
=-$\frac{\frac{sinα}{cosα}•cosa}{sina}$=-1;
(2)原式=$\frac{sin70°}{cos70°}•cos10°•(\frac{\sqrt{3}sin20°}{cos20°}-1)$
=$\frac{sin70°}{cos70°}•cos10°•\frac{\sqrt{3}sin20°-cos20°}{cos20°}$
=$\frac{cos20°}{sin20°}•cos10°•\frac{2sin(20°-30°)}{cos20°}$
=$cos10°•\frac{2sin(-10°)}{sin20°}$=$\frac{-sin20°}{sin20°}$=-1.
点评 本题考查了诱导公式,商的关系,两角差的正弦公式,以及二倍角的正弦公式的应用,考查化简、变形能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 存在正数x0,当x>x0时,2x>x3 | B. | 存在正数x0,当x>x0时,x>lnx | ||
| C. | ?x>2,2x>x2 | D. | ?x>2,x3>$\sqrt{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 买1张肯定不中奖 | B. | 买1000张一定能中奖 | ||
| C. | 买1000张也不一定能中奖 | D. | 买1000张一定恰有1张能中奖 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
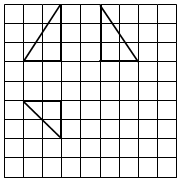 如图,网络纸上正方形的边长为l,粗线画出的是某几何体的三视图,则该几何体的外接球表面积为( )
如图,网络纸上正方形的边长为l,粗线画出的是某几何体的三视图,则该几何体的外接球表面积为( )| A. | 12π | B. | 34π | C. | $\frac{17π}{4}$ | D. | 17π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M、N分别是EF、BC的中点,AB=2AF=2,∠CBA=60°.
如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M、N分别是EF、BC的中点,AB=2AF=2,∠CBA=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC、AD的中点
如图已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC、AD的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某商场连续10天对甲商品每天的销售量(单位:件)进行了统计,得到如图所示的茎叶图,据该图估计商店一天的销售量不低于40件的频率为( )
某商场连续10天对甲商品每天的销售量(单位:件)进行了统计,得到如图所示的茎叶图,据该图估计商店一天的销售量不低于40件的频率为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图.观察图形的信息,回答下列问题.
某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图.观察图形的信息,回答下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{16}{3}$ | B. | 32 | C. | $\frac{32}{3}$ | D. | $\frac{64}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com