
【题目】某公司为了解所经销商品的使用情况,随机问卷50名使用者,然后根据这50名的问卷评分数据,统计得到如图所示的频率布直方图,其统计数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
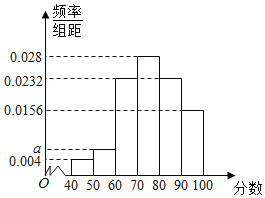
(1)求频率分布直方图中a的值;
(2)求这50名问卷评分数据的中位数;
(3)从评分在[40,60)的问卷者中,随机抽取2人,求此2人评分都在[50,60)的概率.
【答案】(1)0.006;(2)76;(3)![]() .
.
【解析】
(1)由![]() 即可求得;(2)设中位数为
即可求得;(2)设中位数为![]() ,由
,由![]() 即可求得;(3)先分别求出
即可求得;(3)先分别求出![]() 、
、![]() 内的人数,再按古典概型的概率计算公式计算即可.
内的人数,再按古典概型的概率计算公式计算即可.
(1)由频率分布直方图,可得(0.004+a+0.0156+0.0232+0.0232+0.028)×10=1,
解得a=0.006.
(2)由频率分布直方图,可设中位数为m,
则有(0.004+0.006+0.0232)×10+(m﹣70)×0.028=0.5,
解得中位数m=76.
(3)由频率分布直方图,可知在[40,50)内的人数:0.004×10×50=2,
在[50,60)内的人数:0.006×10×50=3.
设在[40,50)内的2人分别为a1,a2,在[50,60)内的3人分别为B1,B2,B3,
则从[40,60)的问卷者中随机抽取2人,基本事件有10种,分别为:
(a1,a2),(a1,B1),(a1,B2),(a1,B3),(a2,B1),
(a2,B2),(a2,B3),(B1,B2),(B1,B3),(B2,B3),
其中2人评分都在[50,60)内的基本事件有(B1,B2),(B1,B3),(B2,B3)共3种,
故此2人评分都在[50,60)的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图1,在边长为3的菱形![]() 中,已知
中,已知![]() ,且
,且![]() .将梯形
.将梯形![]() 沿直线
沿直线![]() 折起,使
折起,使![]() 平面
平面![]() ,如图2,
,如图2,![]() 分别是
分别是![]() 上的点.
上的点.

(1)求证:图2中,平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定数列![]() ,若满足
,若满足![]() (
(![]() 且
且![]() ),对于任意
),对于任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为指数数列.
为指数数列.
(1)已知数列![]() 、
、![]() 的通项公式分别为
的通项公式分别为![]() ,
,![]() ,试判断
,试判断![]() 、
、![]() 是不是指数数列(需说明理由);
是不是指数数列(需说明理由);
(2)若数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,证明:
,证明:![]() 是指数数列;
是指数数列;
(3)若![]() 是指数数列,
是指数数列,![]() ,证明:数列
,证明:数列![]() 中任意三项都不能构成等差数列.
中任意三项都不能构成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的右顶点到其一条渐近线的距离等于
的右顶点到其一条渐近线的距离等于![]() ,抛物线
,抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的右焦点重合,则抛物线
的右焦点重合,则抛物线![]() 上的动点
上的动点![]() 到直线
到直线![]() 和
和![]() 距离之和的最小值为( )
距离之和的最小值为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平行四边形![]() 中,
中,![]() 点
点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]()
(1)求证; 平面![]() 平面
平面![]() ;
;
(2)若平面![]() 和平面
和平面![]() 的交线为
的交线为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂用甲、乙两种不同工艺生产一大批同一种零件,零件尺寸均在[21.7,22.3](单位:cm)之间的零件,把零件尺寸在[21.9,22.1)的记为一等品,尺寸在[21.8,21.9)![]() [22.1,22.2)的记为二等品,尺寸在[21.7,21.8)
[22.1,22.2)的记为二等品,尺寸在[21.7,21.8)![]() [22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示:
[22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示:
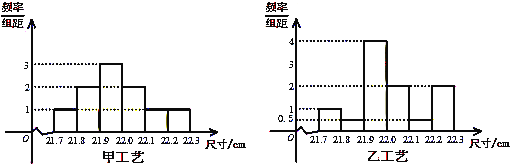
(Ⅰ)根据上述数据完成下列2×2列联表,根据此数据你认为选择不同的工艺与一等品产出率是否有关?
甲工艺 | 乙工艺 | 总计 | |
一等品 | |||
非一等品 | |||
总计 |
P(K2≥k) | 0.1 | 0.05 | 0.01 |
k | 2.706 | 3.841 | 6.635 |
附:![]() ,其中
,其中![]() .
.
(Ⅱ)以上述两种工艺中各种产品的频率作为相应产品产出的概率,若一等品、二等品、三等品的单件利润分别为30元、20元、15元,从一件产品的平均利润考虑,你认为以后该工厂应该选择哪种工艺生产该种零件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论:
①![]() ②
②![]() 是等边三角形 ③AB与平面BCD所成的角是
是等边三角形 ③AB与平面BCD所成的角是![]() ④AB与CD所成角为
④AB与CD所成角为![]() ,其中错误的结论个数是( )
,其中错误的结论个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知中心在原点,顶点A1、A2在x轴上,其渐近线方程是![]() ,双曲线过点
,双曲线过点![]()
(1)求双曲线方程
(2)动直线![]() 经过
经过![]() 的重心G,与双曲线交于不同的两点M、N,问:是否存在直线
的重心G,与双曲线交于不同的两点M、N,问:是否存在直线![]() ,使G平分线段MN,证明你的结论
,使G平分线段MN,证明你的结论
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com