
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
,![]() ,以
,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,连接
,连接![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 为
为![]() .
.
求证:平面![]() 平面
平面![]() ;
;
求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
【答案】(1)证明见解析;(2)①证明见解析,②![]() .
.
【解析】试题分析:(1)先证明四边形![]() 为平行四边形,从而可得
为平行四边形,从而可得![]() ,根据直线与平面平行的判定定理可得
,根据直线与平面平行的判定定理可得![]() 平面
平面![]() ;(2)设
;(2)设![]() 中点为
中点为![]() ,先证明
,先证明![]() 是二面角
是二面角![]() 为
为![]() ,由此可计算出
,由此可计算出![]() 的值,根据勾股定理可得,
的值,根据勾股定理可得,![]()
![]() ,从而可得
,从而可得![]() 平面
平面![]() ,进而可得结果;利用
,进而可得结果;利用![]() 平面
平面![]() ,可得
,可得![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,利用直角三角形的性质可得结果.
所成的角,利用直角三角形的性质可得结果.
试题解析:(1)连接![]()
![]() 且
且![]() ,
,
所以四边形![]() 为平行四边形
为平行四边形 ![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
, ![]()
![]() //平面
//平面![]() ,
,
(2)①取![]() 中点M,连接
中点M,连接![]()
![]()
![]()
![]() ,
,
又![]()
![]() 为二面角的平面角
为二面角的平面角 ![]() ,
,
![]() 中,
中,![]() ,
,
![]()
![]() ,
,
又![]()
![]() ,
, ![]() 平面
平面 ![]()
又![]() ,
, ![]() 平面
平面![]() ,
,![]() 平面
平面![]() , 所以平面
, 所以平面![]() 平面
平面 ![]()
②![]() ,
,![]() 平面
平面![]() 所成角与
所成角与![]() 平面
平面![]() 所成角相等,
所成角相等,
由(2)知 , ![]() 平面
平面![]()
![]() 为线
为线![]() 在平面
在平面![]() 内的射影,
内的射影,
![]() 为直线
为直线![]() 与平面
与平面![]() 所成角,
所成角,
在 ![]() 中,
中, 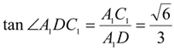 ,
,
![]() 直线
直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]()
【方法点晴】本题主要考查线面平行的判定定理、直线和平面成的角的定义及求法、二面角的求法,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】已知命题![]() :关于
:关于![]() 的不等式
的不等式![]() 无解;命题
无解;命题![]() :指数函数
:指数函数![]() 是增函数.
是增函数.
(1)若命题![]() 为真命题,求
为真命题,求![]() 的取值范围;
的取值范围;
(2)若满足![]() 为假命题
为假命题![]() 为真命题的实数
为真命题的实数![]() 取值范围是集合
取值范围是集合![]() ,集合
,集合![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:
①数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …的一个通项公式是
…的一个通项公式是![]() ;
;
②当![]() 时,不等式
时,不等式![]() 对一切实数x都成立;
对一切实数x都成立;
③函数![]() 是周期为
是周期为![]() 的奇函数;
的奇函数;
④两两相交且不过同一点的三条直线必在同一个平面内.
其中,正确说法序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学学习习惯不好,把黑板上老师写的表达式忘了,记不清楚是![]() 还是
还是![]() .翻出草稿本发现在用五点作图法列表作图时曾算出过一些数据(如下表).
.翻出草稿本发现在用五点作图法列表作图时曾算出过一些数据(如下表).
| 0 |
|
|
| |
|
|
|
|
| |
| 0 | 3 | 0 | 0 |
(1)请你帮助该同学补充完表格中的数据,写出该函数的表达式![]() ,并写出该函数的最小正周期;
,并写出该函数的最小正周期;
(2)若利用![]() 的图象用图象变化法作
的图象用图象变化法作![]() 的图象,其步骤如下:(在空格内填上合适的变换方法)
的图象,其步骤如下:(在空格内填上合适的变换方法)
第一步:![]() 的图象向右平移
的图象向右平移![]() _____得到
_____得到![]() _____的图象;
_____的图象;
第二步:![]() 的图象(纵坐标不变)______得到
的图象(纵坐标不变)______得到![]() _____的图象;
_____的图象;
第三步:![]() 的图象(横坐标不变)_____得到
的图象(横坐标不变)_____得到![]() 的图象.
的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知|x|≤2,|y|≤2,点P的坐标为(x,y).
(1)求当x,y∈R时,P满足(x-2)2+(y-2)2≤4的概率.
(2)求当x,y∈Z时,P满足(x-2)2+(y-2)2≤4的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com