
分析 (Ⅰ)依题意直线AB的斜率为-1,可得直线AB的方程,根据圆心0(0,0)到直线AB的距离,由弦长公式求得AB的长.
(Ⅱ)当弦AB被点M平分时,OM⊥AB,故AB 的斜率为$\frac{1}{2}$,根据点斜式方程直线AB的方程.
解答 解:(Ⅰ) 当$α=\frac{3}{4}π$时,直线AB的方程为:y-2=-(x+1)⇒x+y-1=0
设圆心到直线AB的距离为d,则$d=\frac{{\sqrt{2}}}{2}$
∴$|{AB}|=2\sqrt{{r^2}-{d^2}}=\sqrt{30}$;
(Ⅱ)当弦AB被点M平分时,OM⊥AB.
因为KOM=-2,可得${K_{AB}}=\frac{1}{2}$,故直线AB的方程为:$y-2=\frac{1}{2}({x+1})$
即x-2y+5=0.
点评 本题考查用点斜式求直线方程,点到直线的距离公式,弦长公式的应用,求出圆心0(0,0)到直线AB的距离为d,是解题的关键.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{6},\frac{1}{3}]$ | B. | $(\frac{1}{3},1]$ | C. | $[\frac{1}{6},\frac{1}{3})$ | D. | $[\frac{1}{3},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | $\frac{1}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
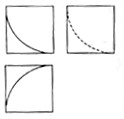 如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为90°的圆弧,则该几何体的体积是( )
如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为90°的圆弧,则该几何体的体积是( )| A. | 1-$\frac{π}{12}$ | B. | 1-$\frac{π}{3}$ | C. | 1-$\frac{π}{6}$ | D. | 1-$\frac{π}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,5] | B. | $[{5,\frac{35}{4}}]$ | C. | $[{0,\frac{35}{4}}]$ | D. | [6,9] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com