《国家中长期教育改革和发展规划纲要》下设A、B、C三个工作组,其分别有组员36,36,18人,现在意见稿已公布,并向社会公开征求意见,为搜集所征求的意见,拟采用分层抽样的方法从A、B、C三个工作小组抽取5名工作人员来完成.
(Ⅰ)求从三个工作组分别抽取的人数;
(Ⅱ)搜集意见结束后,若从抽取的5名工作人员中再随机抽取2名进行汇总整理,求这两名工作人员没有A组工作人员的概率.
【答案】
分析:(I)先求出每个个体被抽到的概率,用每一层的个体数乘以每个个体被抽到的概率,等于该层应抽取的个体数.
(II)设A
1,A
2为从A组抽得的2名工作人员,B
1,B
2为从B组抽得的工作人员,C
1为从C组抽得的工作人员,若从这5名工作人员中随机抽取2名,
写出其所有可能的结果,得到其个数,找出其中没有A组工作人员的结果,得到其的个数,从而得到没有A组工作人员的概率.
解答:解:(I)三个工作组的总人数为36+36+18=90,样本空量与总体中个体数的比为
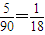
,36×
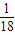
=2,18×
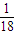
=1.
所以从A、B、C三个工作组分别抽取的人数为2、2、1 …(6分)
(II)设A
1,A
2为从A组抽得的2名工作人员,B
1,B
2为从B组抽得的工作人员,C
1为从C组抽得的工作人员,若从这5名工作人员中随机抽取2名,
其所有可能的结果是:(A
1,A
2),(A
1,B
1),(A
1,B
2),(A
1,C
1),(A
2,B
1),(A
2,B
2),(A
2,C
1),(B
1,B
2),(B
1,C
1),(B
2,C
1),
共有10种,其中没有A组工作人员的结果有3种,所以所求的概率

.…(13分)
点评:本题主要考查分层抽样的定义和方法,等可能事件的概率的求法,用列举法求出所有的基本事件,是解题的关键.

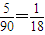 ,36×
,36×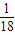 =2,18×
=2,18×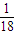 =1.
=1. .…(13分)
.…(13分)

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案