
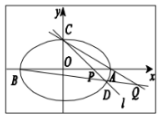
 过点C(0,$\sqrt{2}$)的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,椭圆与x轴交于两点A(a,0),B(-a,0),过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与BD交于点Q.
过点C(0,$\sqrt{2}$)的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,椭圆与x轴交于两点A(a,0),B(-a,0),过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与BD交于点Q.分析 (1)由过点C(0,$\sqrt{2}$)的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,列出方程组,求出a,b,由此能求出椭圆的方程.
(2)椭圆的右焦点为($\sqrt{2}$,0),直线l的方程为y=-x+$\sqrt{2}$,代入椭圆方程化简,得$3{x}^{2}-4\sqrt{2}x=0$,由此能求出|CD|.
(3)当直线l与x轴垂直时,与题意不符.当直线l与x轴不垂直时,设直线l的方程为y=kx+$\sqrt{2}$,(k≠0,且k≠$\frac{\sqrt{2}}{2}$),代入椭圆方程,化简得(2k2+1)x2+4$\sqrt{2}kx$=0,求出D($\frac{-4\sqrt{2}k}{2{k}^{2}+1},\frac{-2\sqrt{2}{k}^{2}+2}{2{k}^{2}+1}$),从而得到kBD,进而求出直线BD的方程,再由直线AC的方程联立$\left\{\begin{array}{l}{y=\frac{\sqrt{2}k+1}{\sqrt{2}-2k}(x+2)}\\{\frac{x}{2}+\frac{y}{\sqrt{2}}=1}\end{array}\right.$,求出Q(-2$\sqrt{2}k$,2k+$\sqrt{2}$),由l方程得P(-$\frac{\sqrt{2}}{k}$,0),由此能证明$\overrightarrow{OP}$•$\overrightarrow{OQ}$为定值.
解答 解:(1)∵ 过点C(0,$\sqrt{2}$)的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,
过点C(0,$\sqrt{2}$)的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,
∴$\left\{\begin{array}{l}{b=\sqrt{2}}\\{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=$\sqrt{2}$,c=$\sqrt{2}$,
∴椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$.
(2)椭圆的右焦点为($\sqrt{2}$,0),
此时直线l的方程为y=-x+$\sqrt{2}$,
代入椭圆方程化简,得$3{x}^{2}-4\sqrt{2}x=0$,
解得${x}_{1}=0,{x}_{2}=\frac{4\sqrt{2}}{3}$,
代入直线l的方程,得${y}_{1}=\sqrt{2}$,y2=-$\frac{\sqrt{2}}{3}$,
∴|CD|=$\sqrt{(\frac{4\sqrt{2}}{3}-0)^{2}+(-\frac{\sqrt{2}}{3}-\sqrt{2})^{2}}$=$\frac{8}{3}$.
证明:(3)当直线l与x轴垂直时,
∵椭圆与x轴交于两点A(a,0),B(-a,0),∴AC∥BD,与题意不符.
设直线l的方程为y=kx+$\sqrt{2}$,(k≠0,且k≠$\frac{\sqrt{2}}{2}$),
代入椭圆方程,化简得(2k2+1)x2+4$\sqrt{2}kx$=0,
解得${x}_{1}=0,{x}_{2}=\frac{-4\sqrt{2}k}{2{k}^{2}+1}$,
代入直线l的方程,得${y}_{1}=\sqrt{2}$,${y}_{2}=\frac{-2\sqrt{2}{k}^{2}+\sqrt{2}}{2{k}^{2}+1}$,
∴D($\frac{-4\sqrt{2}k}{2{k}^{2}+1},\frac{-2\sqrt{2}{k}^{2}+2}{2{k}^{2}+1}$),
∴kBD=$\frac{\frac{-2\sqrt{2}{k}^{2}+\sqrt{2}}{2{k}^{2}+1}}{\frac{-4\sqrt{2}k}{2{k}^{2}+1}+2}$=$\frac{\sqrt{2}(1-2{k}^{2})}{2-4\sqrt{2}k+4{k}^{2}}$=$\frac{\sqrt{2}(1-\sqrt{2}k)(1+\sqrt{2}k)}{(\sqrt{2}-2k)^{2}}$
=$\frac{(\sqrt{2}-2k)(1+\sqrt{2}k)}{(\sqrt{2}-2k)^{2}}$=$\frac{1+\sqrt{2}k}{\sqrt{2}-2k}$,
∴直线BD的方程为y=$\frac{\sqrt{2}k+1}{\sqrt{2}-2k}$(x+2),
又直线AC的方程为$\frac{x}{2}+\frac{y}{\sqrt{2}}=1$,
联立$\left\{\begin{array}{l}{y=\frac{\sqrt{2}k+1}{\sqrt{2}-2k}(x+2)}\\{\frac{x}{2}+\frac{y}{\sqrt{2}}=1}\end{array}\right.$,得$\left\{\begin{array}{l}{x=-2\sqrt{2}k}\\{y=2k+\sqrt{2}}\end{array}\right.$,∴Q(-2$\sqrt{2}k$,2k+$\sqrt{2}$),
又由l方程得P(-$\frac{\sqrt{2}}{k}$,0),
∴$\overrightarrow{OP}•\overrightarrow{OQ}$=(-$\frac{\sqrt{2}}{k},0$)•(-2$\sqrt{2}k$,2k+$\sqrt{2}$)=4.
∴$\overrightarrow{OP}$•$\overrightarrow{OQ}$为定值4.
点评 本题考查椭圆方程的求法,考查线段长的求法,考查向量数量积为定值的证明,是中档题,解题时要认真审题,注意椭圆、直线方程、向量数量积等知识点的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | [1,3] | B. | [$\frac{1}{2}$,$\frac{11}{4}$] | C. | [$\frac{3}{4}$,3] | D. | [$\frac{3}{4}$,$\frac{11}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
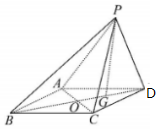 四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{PG}$=$\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+\frac{2}{3}\overrightarrow{c}$.
四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{PG}$=$\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+\frac{2}{3}\overrightarrow{c}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 月份 | 用气量 | 煤气费 |
| 一月份 | 4m3 | 4元 |
| 二月份 | 25m3 | 14元 |
| 三月份 | 35m3 | 19元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com