练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，△ABC为直角三角形，∠C＝90°，，点M在y轴上，且，点C在x轴上移动．

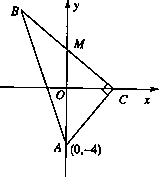
    (Ⅰ)求点B的轨迹E的方程；

    (Ⅱ)过点的直线l与曲线E交于P，Q两点，设N(0，a)(a＜0)，的夹角为，求实数a的取值范围；

    (Ⅲ)设以点N(0，m)为圆心，以为半径的圆与曲线E在第一象限的交点为H，若圆在点H处的切线与曲线E在点H处的切线互相垂直，求实数m的值．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

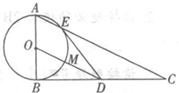    精英家教网4-1（几何证明选讲）
    如图，△ABC是直角三角形，∠ABC=90o．以AB为直径的圆0交AC于点E点D是BC边的中点，连0D交圆0于点M
    （I）求证：0，B，D，E四点共圆；
    （II）求证：2DE2=DM•AC+DM•AB

    查看答案和解析>>

    科目：高中数学 来源： 题型：

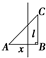    如图，△ABC为等腰直角三角形，直线l与AB相交且l⊥AB，直线l截这个三角形所得的位于直线在右方的图形面积为y，点A到直线l的距离为x，则y=f（x）的图象大致为四个选项中的（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2014•兰州一模）【选修4-1：几何证明选讲】
    如图，△ABC是直角三角形，∠ABC=90°，以AB为直径的圆O交AB于点E，点D是BC边的中点，连接OD交圆O于点M．
    （1）求证：O、B、D、E四点共圆；
    （2）求证：2DE2=DM•AC+DM•AB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

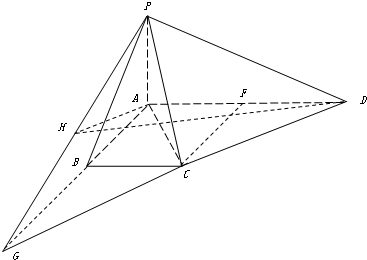    如图，ABCD为直角梯形，∠DAB=∠ABC=90°，AB=BC=1，AD=2，PA⊥平面ABCD，PA=1．
    （1）求点P到CD的距离；
    （2）求证：平面PAC⊥平面PCD；
    （3）求平面PAB与平面PCD所成二面角的大小．

    查看答案和解析>>

    同步练习册答案