
【题目】在平面直角坐标系内,已知点![]() 及线段
及线段![]() ,在线段
,在线段![]() 上任取一点
上任取一点![]() ,线段
,线段![]() 长度的最小值称为“点
长度的最小值称为“点![]() 到线段
到线段![]() 的距离”,记为
的距离”,记为![]() .
.
(1)设点![]() ,线段
,线段![]()
![]() ,求
,求![]() ;
;
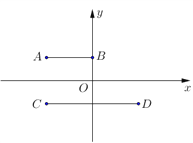
(2)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,线段
,线段![]() ,线段
,线段![]() ,若点
,若点![]() 满足
满足![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出该函数的值域.
的函数解析式,并写出该函数的值域.
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,Sn是数列{an}的前n项和,且4Sn=an2+2an﹣3.
(1)求数列{an}的通项公式;
(2)已知bn=2n,求Tn=a1b1+a2b2+…+anbn的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展,某城市的市民收入逐年增长,表1是该城市某银行连续五年的储蓄存款额(年底余额):
表1
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款额y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将表1的数据进行了处理,令t=x-2 010,z=y-5,得到表2:
表2
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(1)z关于t的线性回归方程是________;y关于x的线性回归方程是________;
(2)用所求回归方程预测到2020年年底,该银行储蓄存款额可达________千亿元.
(附:线性回归方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =
=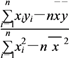 ,
,![]() =
=![]() -
-![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨,硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨,硝酸盐15吨.现库存磷酸盐10吨,硝酸盐66吨,在此基础上生产这两种混合肥料.如果生产1车皮甲种肥料产生的利润为12 000元,生产1车皮乙种肥料产生的利润为7 000元,那么可产生的最大利润是( )
A. 29 000元 B. 31 000元 C. 38 000元 D. 45 000元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)己知函数f(x)= ![]()
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求证:当x∈(0,1)时,f(x)>2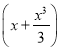
(3)设实数k使得f(x)>k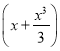 对x∈(0,1)恒成立,求k的最大值.
对x∈(0,1)恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】园林管理处拟在公园某区域规划建设一半径为![]() 米圆心角为
米圆心角为![]() (弧度)的扇形景观水池,其中
(弧度)的扇形景观水池,其中![]() 为扇形
为扇形![]() 的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过
的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过![]() 万元,水池造价为每平方米
万元,水池造价为每平方米![]() 元,步道造价为每米
元,步道造价为每米![]() 元.
元.
(1)当![]() 和
和![]() 分别为多少时,可使广场面积最大,并求出最大值;
分别为多少时,可使广场面积最大,并求出最大值;
(2)若要求步道长为![]() 米,则可设计出水池最大面积是多少.
米,则可设计出水池最大面积是多少.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com