
【题目】某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
(Ⅰ)请在图中补全频率分布直方图;
(Ⅱ)若Q大学决定在成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进行面试.
①若Q大学本次面试中有B、C、D三位考官,规定获得两位考官的认可即面试成功,且面试结果相互独立,已知甲同学已经被抽中,并且通过这三位考官面试的概率依次为 ![]() 、
、 ![]() ,
, ![]() ,求甲同学面试成功的概率;
,求甲同学面试成功的概率;
②若Q大学决定在这6名学生中随机抽取3名学生接受考官B的面试,第3组中有ξ名学生被考官B面试,求ξ的分布列和数学期望.
【答案】解:(Ⅰ)∵第四组的人数为60,
∴总人数为:5×60=300,
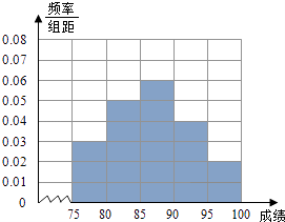
由直方图可知,第五组人数为:0.02×5×300=30人,
又 ![]() 为公差,
为公差,
∴第一组人数为:45人,第二组人数为:75人,第三组人数为:90人(4分)
(Ⅱ)①设事件A=甲同学面试成功,
则P(A)= ![]() ..
..
②由题意得,ξ=0,1,2,3,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
分布列为:
ξ | 0 | 1 | 2 | 3 |
P | | | | |
![]()
【解析】(Ⅰ)由第四组的人数能求出总人数,由此能补全频率分布直方图.(Ⅱ)①设事件A=甲同学面试成功,由此利用独立事件概率公式能求出甲同学面试成功的概率.②由题意得,ξ=0,1,2,3,分别求出其概率,由此能求出ξ的分布列和数学期望.
【考点精析】掌握分层抽样和频率分布直方图是解答本题的根本,需要知道先将总体中的所有单位按照某种特征或标志(性别、年龄等)划分成若干类型或层次,然后再在各个类型或层次中采用简单随机抽样或系用抽样的办法抽取一个子样本,最后,将这些子样本合起来构成总体的样本;频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax+b.
(1)若f(x)在x=2有极小值1﹣e2 , 求实数a,b的值.
(2)若f(x)在定义域R内单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上存在导数f′(x),x∈R,有f(﹣x)+f(x)=x2 , 在(0,+∞)上f′(x)<x,若f(4﹣m)﹣f(m)≥8﹣4m.则实数m的取值范围为( )
A.[﹣2,2]
B.[2,+∞)
C.[0,+∞)
D.(﹣∞,﹣2]∪[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的参数方程 ![]() (φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线l的极坐标方程是2ρsin(θ+ ![]() )=3
)=3 ![]() ,射线OM:θ=
,射线OM:θ= ![]() 与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F2 , P分别为双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的右焦点与右支上的一点,O为坐标原点,若
=1(a>0,b>0)的右焦点与右支上的一点,O为坐标原点,若 ![]() =
= ![]() (
( ![]() +
+ ![]() ),
), ![]() =
= ![]() 且2
且2 ![]()
![]() =a2+b2 , 则该双曲线的离心率为( )
=a2+b2 , 则该双曲线的离心率为( )
A.![]()
B.![]()
C.![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|,其中a>1
(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;
(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆 ![]() (a>b>0)的左右顶点分别是A(﹣
(a>b>0)的左右顶点分别是A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),离心率为
,0),离心率为 ![]() .设点P(a,t)(t≠0),连接PA交椭圆于点C,坐标原点是O.
.设点P(a,t)(t≠0),连接PA交椭圆于点C,坐标原点是O.
(Ⅰ)证明:OP⊥BC;
(Ⅱ)若三角形ABC的面积不大于四边形OBPC的面积,求|t|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图直三棱柱ABC﹣A1B1C1 中AC=2AA1 , AC⊥BC,D、E 分别为A1C1、AB 的中点.求证: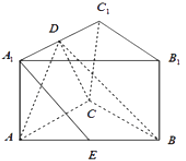
(1)AD⊥平面BCD
(2)A1E∥平面BCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com