
【题目】某学校对任课教师的年龄状况和接受教育程度(学历)做调研,其部分结果(人数分布)如表:
学历 | 35岁以下 | 35~50岁 | 50岁以上 |
本科 | 80 | 30 | 20 |
研究生 | x | 20 | y |
(1)用分层抽样的方法在35~50岁年龄段的教师中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有1人的学历为研究生的概率;
(2)若按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取出1人,此人的年龄为50岁以上的概率为![]() ,求x、y的值.
,求x、y的值.
【答案】(1)![]() (2)x=40,y=5
(2)x=40,y=5
【解析】
试题分析:(1)由题意得:抽到35岁至50岁本科生3人,研究生2人,由此利用列举法能求出从中任取2人,至少有l人的学历为研究生的概率.(2)由题意得:![]() ,由此能求出N,从而能求出x,y的值
,由此能求出N,从而能求出x,y的值
试题解析:(1)用分层抽样的方法在35~50岁中抽取一个容量为5的样本,设抽取学历为本科的人数为m,∴![]() ,解得m=3.
,解得m=3.
∴抽取了学历为研究生的2人,学历为本科的3人,
分别记作S1、S2;B1、B2、B3.
从中任取2人的所有基本事件共10个:
(S1,B1),(S1,B2),(S1,B3),(S2,B1),(S2,B2),(S2,B3),(S1,S2),(B1,B2),
(B2,B3),(B1,B3).
其中至少有1人的学历为研究生的基本事件有7个:(S1,B1),(S1,B2),(S1,B3),
(S2,B1),(S2,B2),(S2,B3),(S1,S2).
∴从中任取2人,至少有1人的教育程度为研究生的概率为![]()
(2)依题意得:![]() ,解得N=78.
,解得N=78.
∴35~50岁中被抽取的人数为78-48-10=20.
∴ ![]() ,解得x=40,y=5.∴x=40,y=5.
,解得x=40,y=5.∴x=40,y=5.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,过点
中,过点![]() 的直线与抛物线
的直线与抛物线![]() 相交于点
相交于点![]() ,
,![]() 两点,设
两点,设![]() ,
,![]()
(1)求证:![]() 为定值
为定值
(2)是否存在平行于![]() 轴的定直线被以
轴的定直线被以![]() 为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长,如果不存在,说明理由.
为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长,如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
A. 792 B. 693 C. 594 D. 495
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=![]() ,动点D在线段AB上.
,动点D在线段AB上.
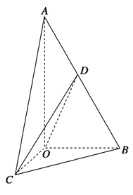
(1)求证:平面COD⊥平面AOB;
(2)当OD⊥AB时,求三棱锥C-OBD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的5次预寒成绩记录如下:
甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用茎叶图表示这两组数据;
(2)求甲、乙两人成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适,说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂以![]() 千克/小时的速度匀速生产某种产品(生产条件要求
千克/小时的速度匀速生产某种产品(生产条件要求![]() ),每一小时可获得的利润是
),每一小时可获得的利润是![]() 元.
元.
(1)要使生产该产品2小时获得的利润不低于1500元,求![]() 的取值范围;
的取值范围;
(2) 要使生产480千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com