
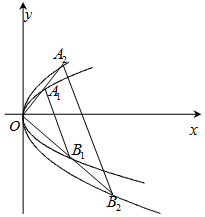
 如图,过原点O引两条直线l1,l2与抛物线W1:y2=2px和W2:y2=4px(其中P为常数,p>0)分别交于四个点A1,B1,A2,B2.
如图,过原点O引两条直线l1,l2与抛物线W1:y2=2px和W2:y2=4px(其中P为常数,p>0)分别交于四个点A1,B1,A2,B2.分析 (Ⅰ)根据抛物线的性质即可求出答案,
(Ⅱ)设l1:y=k1x,代入抛物线方程,得A1,A2的横坐标分别是$\frac{2p}{{k}_{1}^{2}}$和$\frac{4p}{{k}_{1}^{2}}$,即可得到△OA1B1∽△OA2B2,即A1B1∥A2B2.
(Ⅲ)A(x1,y1)B(x2,y2),直线A1B1方程为x=ty+m1,根据韦达定理和直线垂直的关系得到直线A1B1方程为x=ty+2p,A2B2方程为x=ty+4p,
再根据弦长公式和两直线之间的距离公式,以及梯形的面积公式即可求出答案.
解答 解:(Ⅰ)由已知,抛物线W1,W2的准线分别为x=-$\frac{p}{2}$和x=-p,
所以,抛物线W1,W2准线间的距离为$\frac{p}{2}$
(Ⅱ)设l1:y=k1x,代入抛物线方程,得A1,A2的横坐标分别是$\frac{2p}{{k}_{1}^{2}}$和$\frac{4p}{{k}_{1}^{2}}$.
∴$\frac{|O{A}_{1}|}{|O{A}_{2}|}$=$\frac{\sqrt{\frac{4{P}^{2}}{{k}_{1}^{4}}+\frac{4{p}^{2}}{{k}_{1}^{2}}}}{\sqrt{\frac{16{p}^{2}}{{k}_{1}^{4}}+\frac{16{p}^{2}}{{k}_{1}^{2}}}}$=$\frac{1}{2}$,同理$\frac{|O{B}_{1}|}{|O{B}_{2}|}$=$\frac{1}{2}$,
所以△OA1B1∽△OA2B2,
所以A1B1∥A2B2.
(Ⅲ)设A(x1,y1)B(x2,y2),直线A1B1方程为x=ty+m1,
代入曲线y2=2px,得y2-2pty-2pm1=0,
所以y1+y2=2pt,y1y2=-2pm1.
由l1⊥l2,得x1x2+y1y2=0,又y12=2px1,y22=2px2,
所以$\frac{{y}_{1}^{2}{y}_{2}^{2}}{4{p}^{2}}$+y1y2=0,由y1y2=-2pm1,得m1=2p.
所以直线A1B1方程为x=ty+2p,
同理可求出直线A2B2方程为x=ty+4p,
所以|A1B1|=$\sqrt{1+{t}^{2}}$|y1-y2|=2p$\sqrt{1+{t}^{2}}$•$\sqrt{{t}^{2}+4}$,|A2B2|=4p$\sqrt{1+{t}^{2}}$•$\sqrt{{t}^{2}+4}$,
平行线A1B1与A2B2之间的距离为d=$\frac{2p}{\sqrt{1+{t}^{2}}}$,
所以梯形A1A2B2B1的面积$S=\frac{1}{2}(|{{A_1}{B_1}}|+|{{A_2}{B_2}}|)•d=6{p^2}\sqrt{{t^2}+4}$≥12p2
当t=0时,梯形A1A2B2B1的面积达最小,最小值为12p2.
点评 本题考查了抛物线的性质直线和抛物线的位置关系,考查了学生的运算能力,以及转化能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,E为正四棱锥P-ABCD侧棱PD上异于P,D的一点,给出下列结论:
如图,E为正四棱锥P-ABCD侧棱PD上异于P,D的一点,给出下列结论:| A. | ①②③ | B. | ①③④ | C. | ②④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com