
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 存在两个极值点
存在两个极值点![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
【答案】(1)答案见解析;(2)证明见解析.
【解析】分析:(1)对m分类讨论求函数![]() 的单调区间.(2)先求出
的单调区间.(2)先求出![]() ,再构造函数
,再构造函数![]() ,
,![]() ,求它的范围.
,求它的范围.
详解:(1)函数![]() 定义域为
定义域为![]() ,且
,且![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单调递减;
上单调递减;
当![]() ,即
,即![]() 时,由
时,由![]() ,解得
,解得![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,∴
,∴![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
若![]() ,则
,则![]() ,∴
,∴![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
综上所述:![]() 时,
时,![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;
;
![]() 时,
时,![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() ,单调递增区间为
,单调递增区间为![]() ;
;
![]() 时,
时,![]() 的单调递减区间为
的单调递减区间为![]() .
.
(2)因为函数![]() 定义域为
定义域为![]() ,且
,且![]() ,
,
∵函数![]() 存在两个极值点,∴
存在两个极值点,∴![]() 在
在![]() 上有两个不等实根
上有两个不等实根![]() ,
,![]() ,
,
记![]() ,则
,则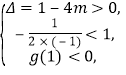 ∴
∴![]() ,
,
从而由![]() 且
且![]() ,可得
,可得![]() ,
,![]() ,
,
∴![]()
![]() ,
,
构造函数![]() ,
,![]() ,
,
则![]() ,
,
记![]() ,
,![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() (
(![]() ,故舍去),
,故舍去),
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
又![]() ,
,![]() ,
,
∴当![]() 时,恒有
时,恒有![]() ,即
,即![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]() ,
,
∴![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】函数![]() 与
与![]() 的图象拼成如图所示的“
的图象拼成如图所示的“![]() ”字形折线段
”字形折线段![]() ,不含
,不含![]()
![]()
![]()
![]()
![]() 五个点,若
五个点,若![]() 的图象关于原点对称的图形即为
的图象关于原点对称的图形即为![]() 的图象,则其中一个函数的解析式可以为__________.
的图象,则其中一个函数的解析式可以为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,任取
,任取![]() ,记函数
,记函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() 最小值为
最小值为![]() 记
记![]() . 则关于函数
. 则关于函数![]() 有如下结论:
有如下结论:
①函数![]() 为偶函数;
为偶函数;
②函数![]() 的值域为
的值域为![]() ;
;
③函数![]() 的周期为2;
的周期为2;
④函数![]() 的单调增区间为
的单调增区间为![]() .
.
其中正确的结论有____________.(填上所有正确的结论序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际上钻石的重量计量单位为克拉;已知某种钻石的价值![]() (美元)与其重量
(美元)与其重量![]() (克拉)的平方成正比,且一颗重为3克拉的该种钻石的价值为54000美元;
(克拉)的平方成正比,且一颗重为3克拉的该种钻石的价值为54000美元;
(1)写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若把一颗钻石切割成重量比为![]() 的两颗钻石,求价值损失的百分率;
的两颗钻石,求价值损失的百分率;
(3)把一颗钻石切割成两颗钻石,若两颗钻石的重量分别为![]() 克拉和
克拉和![]() 克拉,试用你所学的数学知识分析当
克拉,试用你所学的数学知识分析当![]() ,
,![]() 满足何种关系时,价值损失的百分率最大.
满足何种关系时,价值损失的百分率最大.
(注:价值损失的百分率![]() ,在切割过程中重量损耗忽略不计)
,在切割过程中重量损耗忽略不计)
查看答案和解析>>
科目:高中数学 来源: 题型:
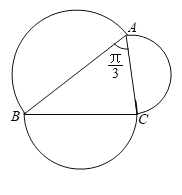
【题目】定义在封闭的平面区域D内任意两点的距离的最大值称为平面区域D的“直径".已知锐角三角形的三个顶点A,B,C在半径为1的圆上,且![]() ,分别以
,分别以![]() 各边为直径向外作三个半圆,这三个半圆和
各边为直径向外作三个半圆,这三个半圆和![]() 构成平面区域D,则平面区域D的“直径”是______.
构成平面区域D,则平面区域D的“直径”是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一商场对5年来春节期间服装类商品的优惠金额![]() (单位:万元)与销售额
(单位:万元)与销售额![]() (单位:万元)之间的关系进行分析研究并做了记录,得到如下表格.
(单位:万元)之间的关系进行分析研究并做了记录,得到如下表格.
日期 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图,并判断服装类商品的优惠金额与销售额是正相关还是负相关;

(2)根据表中提供的数据,求出![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(3)若2019年春节期间商场预定的服装类商品的优惠金额为10万元,估计该商场服装类商品的销售额.
参考公式:
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】司机在开机动车时使用手机是违法行为,会存在严重的安全隐患,危及自己和他人的生命.为了研究司机开车时使用手机的情况,交警部门调查了100名机动车司机,得到以下统计:在55名男性司机中,开车时使用手机的有40人,开车时不使用手机的有15人;在45名女性司机中,开车时使用手机的有20人,开车时不使用手机的有25人.
(1)完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别有关;

(2)以上述的样本数据来估计总体,现交警部门从道路上行驶的大量机动车中随机抽检3辆,记这3辆车中司机为男性且开车时使用手机的车辆数为X,若每次抽检的结果都相互独立,求X的分布列和数学期望E(X).
参考公式与数据:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上给定![]() 及点
及点![]() ,构造点列
,构造点列![]() ,
,![]() ,
,![]() ,…,使得
,…,使得![]() 为点
为点![]() 绕中心
绕中心![]() 顺时针旋转
顺时针旋转![]() 时所到达的位置,而
时所到达的位置,而![]() 和
和![]() 为点
为点![]() 和
和![]() 分别绕中心
分别绕中心![]() 和
和![]() 顺时针旋转
顺时针旋转![]() 时所到达的位置,
时所到达的位置,![]() .若对某个
.若对某个![]() ,有
,有![]() ,试求
,试求![]() 的各个内角的度数及三个顶点
的各个内角的度数及三个顶点![]() ,
,![]() ,
,![]() 的排列方向.
的排列方向.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )(多选)
A.有一个面是多边形,其余各面都是三角形,由这些面围成的多面体是棱锥
B.有两个面平行且相似,其余各面都是梯形的多面体是棱台
C.如果一个棱锥的各个侧面都是等边三角形,那么这个棱锥可能为六棱锥
D.如果一个棱柱的所有面都是长方形,那么这个棱柱是长方体
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com