
【题目】如图四面体ABCD中,△ABC是正三角形,AD=CD.(12分)
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.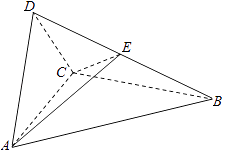
【答案】
(1)
证明:取AC中点O,连结DO、BO,
∵△ABC是正三角形,AD=CD,
∴DO⊥AC,BO⊥AC,
∵DO∩BO=O,∴AC⊥平面BDO,
∵BD平面BDO,∴AC⊥BD.
(2)
解:设AD=CD= ![]() ,则AC=AB=BC=BD=2,AO=CO=DO=1,
,则AC=AB=BC=BD=2,AO=CO=DO=1,
∴BO= ![]() =
= ![]() ,∴BO2+DO2=BD2,∴BO⊥DO,
,∴BO2+DO2=BD2,∴BO⊥DO,
以O为原点,OA为x轴,OB为y轴,OD为z轴,建立空间直角坐标系,
则C(﹣1,0,0),D(0,0,1),B(0, ![]() ,0),A(1,0,0),
,0),A(1,0,0),
设E(a,b,c), ![]() ,(0≤λ≤1),则(a,b,c﹣1)=λ(0,
,(0≤λ≤1),则(a,b,c﹣1)=λ(0, ![]() ,﹣1),解得E(0,
,﹣1),解得E(0, ![]() ,1﹣λ),
,1﹣λ),
∴ ![]() =(1,
=(1, ![]() ),
), ![]() =(﹣1,
=(﹣1, ![]() ),
),
∵AE⊥EC,∴ ![]() =﹣1+3λ2+(1﹣λ)2=0,
=﹣1+3λ2+(1﹣λ)2=0,
由λ∈[0,1],解得 ![]() ,∴DE=BE,
,∴DE=BE,
∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,
∵DE=BE,∴S△DCE=S△BCE,
∴四面体ABCE与四面体ACDE的体积比为1.
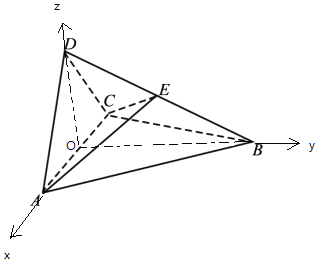
【解析】(1.)取AC中点O,连结DO、BO,推导出DO⊥AC,BO⊥AC,从而AC⊥平面BDO,由此能证明AC⊥BD.
(2.)设AD=CD= ![]() ,则AC=AB=BC=BD=2,AO=CO=DO=1,BO=
,则AC=AB=BC=BD=2,AO=CO=DO=1,BO= ![]() ,推导出BO⊥DO,以O为原点,OA为x轴,OB为y轴,OD为z轴,建立空间直角坐标系,由AE⊥EC,求出DE=BE,由此能求出四面体ABCE与四面体ACDE的体积比.
,推导出BO⊥DO,以O为原点,OA为x轴,OB为y轴,OD为z轴,建立空间直角坐标系,由AE⊥EC,求出DE=BE,由此能求出四面体ABCE与四面体ACDE的体积比.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某零售店近5个月的销售额和利润额资料如下表:
商店名称 |
|
|
|
|
|
销售额 | 3 | 5 | 6 | 7 | 9 |
利润额 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系;
(2)用最小二乘法计算利润额![]() 关于销售额
关于销售额![]() 的回归直线方程;
的回归直线方程;
(3)当销售额为4千万元时,利用(2)的结论估计该零售店的利润额(百万元).
[参考公式: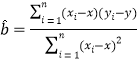 ,
,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况,随机抽查了该市60名网友在该网店的网购金额情况,如下表:
网购金额(单位:千元) | 频数 | 频率 | 网购金额(单位:千元) | 频数 | 频率 | |
[0,0.5) | 3 | 0.05 | [1.5,2) | 15 | 0.25 | |
[0.5,1) |
|
| [2,2.5) | 18 | 0.30 | |
[1,1.5) | 9 | 0.15 | [2.5,3] |
|
|
若将当日网购金额不小于2千元的网友称为“网购达人”,网购金额小于2千元的网友称为“网购探者”,已知“网购达人”与“网购探者”人数的比例为2:3.
(1)确定![]() ,
,![]() ,
,![]() ,
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
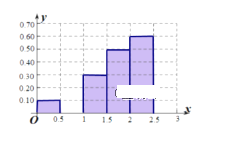
(2)①.试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数;
②.若平均数和中位数至少有一个不低于2千元,则该网店当日评为“皇冠店”,试判断该网店当日能否被评为“皇冠店”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标![]() 中,圆
中,圆![]() ,圆
,圆![]() 。
。
(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆![]() 的极坐标方程,并求出圆
的极坐标方程,并求出圆![]() 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);
(Ⅱ)求圆![]() 的公共弦的参数方程。
的公共弦的参数方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点S、A、B、C在半径为 ![]() 的同一球面上,点S到平面ABC的距离为
的同一球面上,点S到平面ABC的距离为 ![]() ,AB=BC=CA=
,AB=BC=CA= ![]() ,则点S与△ABC中心的距离为( )
,则点S与△ABC中心的距离为( )
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,直线x+y+
,直线x+y+ ![]() =0与椭圆E仅有一个公共点.
=0与椭圆E仅有一个公共点.
(1)求椭圆E的方程;
(2)直线l被圆O:x2+y2=3所截得的弦长为3,且与椭圆E交于A、B两点,求△ABO面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a,b 是函数![]() 的两个不同的零点,且a,b,-2 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q 的值等于( )
的两个不同的零点,且a,b,-2 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q 的值等于( )
A.6
B.7
C.8
D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com