
����Ŀ����![]() �ǹ���Ϊ�����ĵȱ�����,
�ǹ���Ϊ�����ĵȱ�����,![]() ,
,![]()
(1)��![]() ��ͨ�ʽ;
��ͨ�ʽ;
(2)��![]() ������Ϊ1,����Ϊ2�ĵȲ�����,������
������Ϊ1,����Ϊ2�ĵȲ�����,������![]() ��ǰ
��ǰ![]() ���
���![]()
���𰸡���1��![]() ��2��
��2��![]()
��������
(1)![]() ���ݵȱ����е�ͨ�ʽ�õ���
���ݵȱ����е�ͨ�ʽ�õ���![]() ����ö��η��̿ɵõ�
����ö��η��̿ɵõ�![]() ��
��![]() (��ȥ)�������õ����е�ͨ���2����֪���е������ǵȲ�������ȱ�������͵����⣬���ݵȲ�ȱ��������ʽ�õ��������.
(��ȥ)�������õ����е�ͨ���2����֪���е������ǵȲ�������ȱ�������͵����⣬���ݵȲ�ȱ��������ʽ�õ��������.
��:(1)��![]() Ϊ�ȱ�����
Ϊ�ȱ�����![]() �Ĺ���,����
����,����![]() ,
,![]() ��:
��:![]()
��![]() ,���:
,���:![]() ��
��![]() (��ȥ)
(��ȥ)
����![]() ��ͨ�ʽΪ
��ͨ�ʽΪ![]()
(2) �� �� �� �� �� �� ͨ �� �� ʽ �� ����![]()
�� �� �� �� ���� �� �� ʽ �� �� �� �� �� ǰ n �� �� �� ʽ �� ��
![]()
���㾦��
�����Ŀ�����������ͨ�ʽ����������͵ij��÷���������ͨ��������г�������֪![]() ��
��![]() �Ĺ�ϵ����
�Ĺ�ϵ����![]() ����ʽ��һ����д��
����ʽ��һ����д��![]() �����ͨ��������ַ�����Ҫ����n=1ʱͨ�ʽ�Ƿ����ã�������ͳ��÷��У���λ�����������ͣ�������͵ȡ�
�����ͨ��������ַ�����Ҫ����n=1ʱͨ�ʽ�Ƿ����ã�������ͳ��÷��У���λ�����������ͣ�������͵ȡ�
�����͡������
��������
18
����Ŀ����a��b�������x�IJ���ʽa2x��b2(1��x)��[ax��b(1��x)]2��
 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�����꼶��ѧ��1000���������飬����750��ͬѧ�����μ�������������ΪA��ͬѧ��������250��ͬѧ�������μ�������������ΪB��ͬѧ�������÷ֲ������������A�ࡢB������㣩�Ӹ��꼶��ѧ���г��100��ͬѧ����������ߴﵽ165������Ϊ���ı����Գ�ȡ��100��ѧ������ͳ�ƣ��õ�������������
���ߴ�� | ���߲���� | �ܼ� | |
������������� | 40 | ||
��������������� | 15 | ||
�ܼ� | 100 |
��1������ϱ���
��2���ܷ��з����ʲ�����0.05��ǰ������Ϊ�������������ߴ���й�ϵ����![]() �Ĺ۲�ֵ��ȷ��0.001����
�Ĺ۲�ֵ��ȷ��0.001����
�ο���ʽ��![]() ��
��
�ο����ݣ�
P��K2��k�� | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ax2+ ![]() +5������a��b��R������f��1��+f����1��=14��
+5������a��b��R������f��1��+f����1��=14��
��1�����a��ֵ�����ͳ���b�IJ�ͬȡֵ���ۺ���f��x����ż�ԣ�
��2����f��x�������䣨���ޣ��� ![]() ���ϵ����ݼ�����b����Сֵ��
���ϵ����ݼ�����b����Сֵ��
��3���ڣ�2���������£���bȡ��Сֵʱ��֤����f��x��ǡ��һ�����q�Ҵ��ڵ���������������{an}��ʹ�� ![]() =q
=q ![]() +q
+q ![]() +q
+q ![]() +��+q
+��+q ![]() +��������
+��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��aΪ��������
��aΪ��������![]() ��ͼ����
��ͼ����![]() .
.
��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2���躯��![]() ����
����![]() ��
��![]() �Ͻ⼯�ǿգ���ʵ��b��ȡֵ��Χ��
�Ͻ⼯�ǿգ���ʵ��b��ȡֵ��Χ��
��3��֤��������![]() ���ҽ���һ���⣮
���ҽ���һ���⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Բ����Բ��϶��ɵļ����������ͼ����ü�����ı����Ϊ�� �� 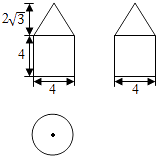
A.20��
B.24��
C.28��
D.32��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD��A1B1C1D1�У�����A1A�͵���ABCD��AB��AC��AB=1��AC=AA1=2��AD=CD= ![]() ���ҵ�M��N�ֱ�ΪB1C��D1D���е㣮
���ҵ�M��N�ֱ�ΪB1C��D1D���е㣮
��I����֤��MN��ƽ��ABCD��
��II��������D1��AC��B1������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x���Ƕ�����R�ϵ��溯������x��0ʱ��f��x��=x��1����ʽf��x����0�Ľ⼯Ϊ�� �� 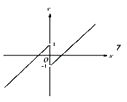
A.�����ޣ���1���ȣ�0��1��
B.�����ޣ���1���ȣ�1��+�ޣ�
C.����1��1��
D.����1��0���ȣ�1��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��֪����![]() �ļ����귽����
�ļ����귽����![]() ���Լ���Ϊԭ�㣬����Ϊ
���Լ���Ϊԭ�㣬����Ϊ![]() ��������Ὠ��ƽ��ֱ������ϵ��ֱ��
��������Ὠ��ƽ��ֱ������ϵ��ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ (
(![]() ������.
������.
(I)д��ֱ��![]() ��һ�㷽��������
��һ�㷽��������![]() ��ֱ�����귽�̣����ж����ǵ�λ�ù�ϵ��
��ֱ�����귽�̣����ж����ǵ�λ�ù�ϵ��
(II)������![]() ����ƽ��
����ƽ��![]() ����λ���ȣ�����ƽ��
����λ���ȣ�����ƽ��![]() ����λ���ȣ��õ�����
����λ���ȣ��õ�����![]() ��������
��������![]() ���������任
���������任![]() �õ�����
�õ�����![]() ��������
��������![]() ����һ��Ϊ
����һ��Ϊ![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊѵ�����ӵ�����������������һ��������װ�б��Ϊ1,2,3,4,5�Ŀ�Ƭ��2�ţ��ú��ӴӺ�������ȡ3�ſ�Ƭ������Ƭ��������ֵ�9���Ʒ֣�ÿ�ſ�Ƭ��ȡ���Ŀ����Զ���ȣ���X��ʾȡ����3�ſ�Ƭ�ϵ��������
(1)��ȡ����3�ſ�Ƭ�ϵ����ֻ�����ͬ�ĸ��ʣ�
(2)���������x�ķֲ��У�
(3)������ȡ���Ŀ�Ƭ�ļƷֳ���30�֣��͵õ����������ӵõ������ĸ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com