
已知直线 ,圆
,圆 .
.
(1)求直线 被圆
被圆 所截得的弦长;
所截得的弦长;
(2)如果过点 的直线
的直线 与直线
与直线 垂直,
垂直, 与圆心在直线
与圆心在直线 上的圆
上的圆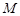 相切,圆
相切,圆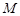 被直线
被直线 分成两段圆弧,且弧长之比为
分成两段圆弧,且弧长之比为 ,求圆
,求圆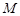 的方程.
的方程.
(1)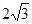 ;(2)
;(2)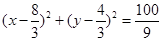 或
或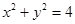 .
.
解析试题分析:(1)由题意可以通过求弦心距进而求得弦长,而弦心距即为圆心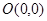 到直线
到直线 的距离:
的距离: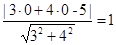 ,再由垂径定理,弦长为
,再由垂径定理,弦长为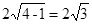 ;(2)根据题意可求得
;(2)根据题意可求得 :
: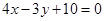 ,由圆心
,由圆心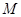 在直线
在直线 上,可设
上,可设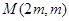 ,从而根据
,从而根据 与圆
与圆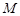 相切可知圆
相切可知圆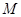 的半径
的半径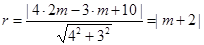 ,再由圆
,再由圆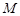 被直线
被直线 分成两段圆弧,且弧长之比为
分成两段圆弧,且弧长之比为 ,可知两段弧的度数分为为
,可知两段弧的度数分为为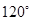 ,
,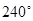 ,从而直线
,从而直线 截圆
截圆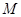 的弦的弦心距为半径的一半,即有关于
的弦的弦心距为半径的一半,即有关于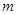 的方程:
的方程: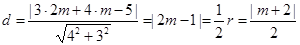 ,解得
,解得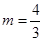 或
或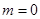 ,从而可得圆
,从而可得圆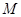 的方程为:
的方程为: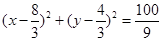 或
或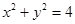 .
.
试题解析:(1)直线 被圆
被圆 所截得弦弦心距为
所截得弦弦心距为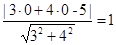 ,∴弦长为
,∴弦长为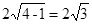 ; 3分
; 3分
∵ 过点
过点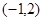 且与
且与 垂直,∴
垂直,∴ :
: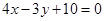 , 3分
, 3分
∵圆心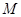 在直线
在直线 上,∴设
上,∴设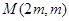 ,∵
,∵ 与圆
与圆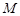 相切,∴
相切,∴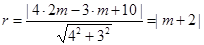 ,
,
设 与圆
与圆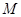 交于
交于 ,
, 两点,∵圆
两点,∵圆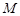 被直线
被直线 分成两段圆弧,且弧长之比为
分成两段圆弧,且弧长之比为 ,∴
,∴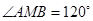 ,
,
即可得 的弦心距
的弦心距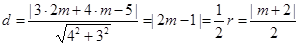 ,解得
,解得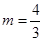 或
或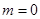 ,
,
∴圆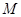 的方程为:
的方程为: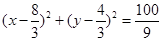 或
或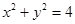 . 6分
. 6分
考点:1.直线与圆的位置关系;2.圆的标准方程.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:填空题
已知圆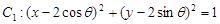 与圆
与圆 ,在下列说法中:
,在下列说法中:
①对于任意的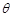 ,圆
,圆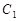 与圆
与圆 始终相切;
始终相切;
②对于任意的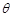 ,圆
,圆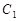 与圆
与圆 始终有四条公切线;
始终有四条公切线;
③当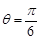 时,圆
时,圆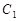 被直线
被直线 截得的弦长为
截得的弦长为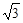 ;
;
④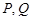 分别为圆
分别为圆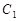 与圆
与圆 上的动点,则
上的动点,则 的最大值为4.
的最大值为4.
其中正确命题的序号为______.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,⊙O内切△ABC的边于D、E、F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.求证:
(1)圆心O在直线AD上;
(2)点C是线段GD的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知圆 的方程:
的方程:
(1)求m的取值范围;
(2)若圆C与直线 相交于
相交于 ,
, 两点,且
两点,且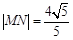 ,求
,求 的值
的值
(3)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com