Question

【题目】在平面直角坐标系xOy中，C1的参数方程为 (t为参数)，在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，C2的极坐标方程ρ2－2ρcos θ－3＝0.

(Ⅰ)说明C2是哪种曲线，并将C2的方程化为普通方程；

(Ⅱ)C1与C2有两个公共点A，B，定点P的极坐标，求线段AB的长及定点P到A，B两点的距离之积．

Answer 1

【答案】(Ⅰ)C2是圆，C2的普通方程是：(x－1)2＋y2＝4.(Ⅱ)答案见解析.

【解析】试题分析：（1）C2是圆，利用极坐标方程与普通方程转化方法，将C2的方程化为普通方程；（2）利用参数的几何意义，求线段AB的长及定点P到A，B两点的距离之积．

试题解析：

(Ⅰ)C2是圆，C2的极坐标方程ρ2－2ρcos θ－3＝0，

化为普通方程：x2＋y2－2x－3＝0即：(x－1)2＋y2＝4.

(Ⅱ)P的极坐标为，

平面直角坐标为(1,1)，在直线C1上，

将C1的参数方程为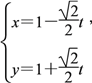(t为参数)

代入x2＋y2－2x－3＝0中得：

2＋2－2－3＝0

化简得：t2＋t－3＝0 设两根分别为t1，t2，

由韦达定理知：

所以AB的长|AB|＝|t1－t2|

＝＝＝，

定点P到A，B两点的距离之积

|PA|·|PB|＝|t1t2|＝3.