【题目】如图，直线
平面
，直线平行四边形
，四棱锥
的顶点
在平面上，
，
，
，
，
分别是
与
的中点.
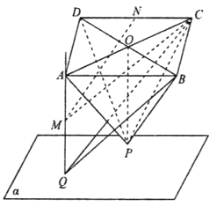
（1）求证：
平面
；
（2）求二面角
的余弦值.
【答案】（1）见解析；（2）
【解析】
（1）连接
，由题意可证得平面
平面
，利用面面平行的性质定理可得
平面；
（2）过
作
，以
所在直线分别为
轴建立空间直角坐标系，由题意可得平面
的法向量为
，平面
的法向量为
，据此计算可得二面角
的平面角
的余弦
.
（1）连接，底面
为平行四边形，
是
的中点，
是
的中点，
，
是
的中点，是
的中点， 
，
，
，平面平面，
平面
， 平面；
（2）由
平面
，平行四边形，
平面
底面，
， 
，
四边形
为矩形，且
底面，
，过作，
以所在直线分别为轴建立空间直角坐标系（如图），
由
，
，，知
，
、
、
、
、
、
，
、
、
，
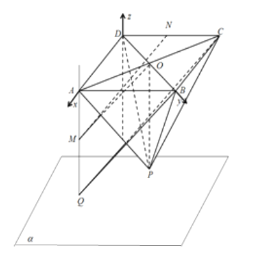
设平面的法向量为
，
则
,
取
，
，
，即，
设平面的法向量为
则
,
取
，
，
，即，
二面角的平面角的余弦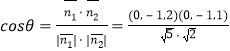
.
科目：高中数学 来源： 题型：
【题目】某地区为调查新生婴儿健康状况，随机抽取6名8个月龄婴儿称量体重（单位：千克），称量结果分别为6，8，9，9，9.5，10.已知8个月龄婴儿体重超过7.2千克，不超过9.8千克为“标准体重”，否则为“不标准体重”.
(1)根据样本估计总体思想，将频率视为概率，若从该地区全部8个月龄婴儿中任取3名进行称重，则至少有2名婴儿为“标准体重”的概率是多少？
(2)从抽取的6名婴儿中，随机选取4名，设X表示抽到的“标准体重”人数，求X的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，三条直线型公路
，
，
在点
处交汇，其中与、与的夹角都为
，在公路上取一点
，且
km，过铺设一直线型的管道
，其中点
在上，点
在上（，足够长），设
km，
km．
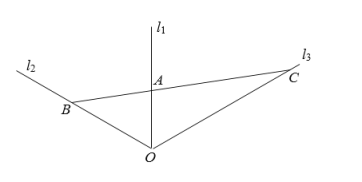
（1）求出
，
的关系式；
（2）试确定，的位置，使得公路
段与
段的长度之和最小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，函数
的图像为直线
．
（Ⅰ）当
时，若函数
的图像永远在直线下方，求实数
的取值范围；
（Ⅱ）当
时，若直线与函数的图像的有两个不同的交点
，线段
的中点为
，求证：
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知倾斜角为
的直线经过抛物线
：
的焦点
，与抛物线相交于
、
两点，且
.
（Ⅰ）求抛物线的方程；
（Ⅱ）过点
的两条直线
、
分别交抛物线于点
、
和
、，线段
和
的中点分别为
、
.如果直线与的倾斜角互余，求证：直线
经过一定点.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某创业团队拟生产
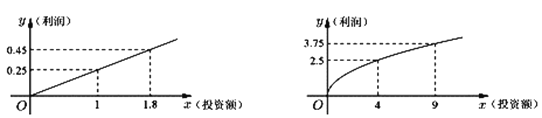
两种产品，根据市场预测，
产品的利润与投资额成正比（如图1），
产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)
（注：利润与投资额的单位均为万元）
(1)分別将两种产品的利润
、
表示为投资额
的函数；
(2)该团队已筹集到10 万元资金，并打算全部投入两种产品的生产，问:当产品的投资额为多少万元时，生产两种产品能获得最大利润，最大利润为多少?
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2017年，在青岛海水稻研究发展宗鑫的试验基地，我国奇数团队培养处的最新一批海水稻活动丰收，由原亩产300公斤，条到最高620公斤，弦长测得其海水盐分浓度月为
。
（1）对
四种品种水稻随机抽取部分数据，获得如下频率分布直方图，根据直方图，说明这四种品种水稻中，哪一种平均产量最高，哪一种稳定（给出判断即可，不必说明理由）；
（2）对盐碱度与抗病害的情况差得如右图和
的列联表的部分数据，填写列表，并以此说明是否有
的把握说明盐碱度对抗病虫害有影响。
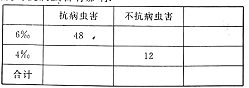
附表及公式：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某船在海面
处测得灯塔
在北偏东
方向，与相距
海里，测得灯塔
在北偏西
方向，与相距
海里，船由向正北方向航行到
处，测得灯塔在南偏西
方向，这时灯塔与相距多少海里？在的什么方向？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
