
【题目】从条件①![]() ,②
,②![]() ,③
,③![]() ,
,![]() 中任选一个,补充到下面问题中,并给出解答.
中任选一个,补充到下面问题中,并给出解答.
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,________.若
,________.若![]() ,
,![]() ,
,![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
【答案】若选择①,![]() ;若选择②,
;若选择②,![]() ;若选择③,
;若选择③,![]() .
.
【解析】
若选择①,利用![]() 可得
可得![]() ,可得
,可得![]() ,再根据等比中项列方程解得
,再根据等比中项列方程解得![]() 即可;若选择②,根据
即可;若选择②,根据![]() 可得
可得![]() ,可得
,可得![]() ,
,![]() ,再根据等比中项列方程解得
,再根据等比中项列方程解得![]() 即可;若选择③,利用
即可;若选择③,利用![]() 可得
可得![]() ,
,![]() ,再根据等比中项列方程解得
,再根据等比中项列方程解得![]() 即可.
即可.
若选择①,
因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
两式相减得![]() ,整理得
,整理得![]() .
.
即![]() ,
,![]() .
.
所以![]() 为常数列.
为常数列.![]() ,所以
,所以![]() .
.
(或由![]() ,利用相乘相消法,求得
,利用相乘相消法,求得![]() )
)
所以![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() 成等比数列,所以
成等比数列,所以![]() ,
,
所以![]() ,解得
,解得![]() 或
或![]() (舍),
(舍),
所以![]() .
.
若选择②,
由![]() 变形得,
变形得,![]() ,
,
所以![]() ,
,
易知![]() ,所以
,所以![]() ,
,
所以![]() 为等差数列,又
为等差数列,又![]() ,所以
,所以![]() ,
,![]() ,
,
∴![]()
![]() ,
,
又![]() 时,
时,![]() 也满足上式,
也满足上式,
所以![]() .
.
因为![]() ,
,![]() ,
,![]() 成等比数列,∴
成等比数列,∴![]() ,
,
∴![]() 或
或![]() ,又
,又![]() ,∴
,∴![]() .
.
若选择③,
因为![]() ,所以
,所以![]() ,
,
两式相减得![]() ,
,
整理得![]() ,
,
因为![]() ,∴
,∴![]() ,所以
,所以![]() 是等差数列,
是等差数列,
所以![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,![]() 成等比数列,∴
成等比数列,∴![]() ,
,
∴![]() 或
或![]() ,又
,又![]() ,∴
,∴![]() .
.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
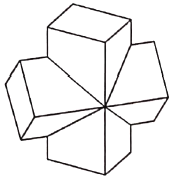
【题目】如图是某机械零件的几何结构,该几何体是由两个相同的直四棱柱组合而成的,且前后、左右、上下均对称,每个四棱柱的底面都是边长为2的正方形,高为4,且两个四棱柱的侧棱互相垂直.则这个几何体有________个面,其体积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,图(a)、图(b)是边长为![]() 的两块正方形钢板,现要将图(a)裁剪焊接成一个正四棱柱,将图(b)裁剪焊接成一个正四棱锥,使它们的全面积都等于这个正方形的面积(不计焊接缝的面积).
的两块正方形钢板,现要将图(a)裁剪焊接成一个正四棱柱,将图(b)裁剪焊接成一个正四棱锥,使它们的全面积都等于这个正方形的面积(不计焊接缝的面积).
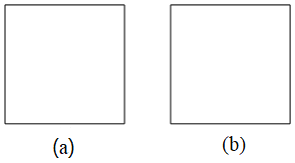
(1)将裁剪方法用虚线标示在图中,并作简要说明;
(2)比较所制成的正四棱柱和正四棱锥体积大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|![]() ),y=f(x)的图象关于直线x
),y=f(x)的图象关于直线x![]() 对称,且与x轴交点的横坐标构成一个公差为
对称,且与x轴交点的横坐标构成一个公差为![]() 的等差数列,则函数f(x)的导函数
的等差数列,则函数f(x)的导函数![]() 的一个单调减区间为( )
的一个单调减区间为( )
A.[![]() ,
,![]() ]B.[
]B.[![]() ,
,![]() ]C.[
]C.[![]() ,
,![]() ]D.[
]D.[![]() ,
,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半圆O的直径AB=2,点C在AB的延长线上,BC=1,点P为半圆上异于A,B两点的一个动点,以点P为直角顶点作等腰直角![]() ,且点D与圆心O分布在PC的两侧,设
,且点D与圆心O分布在PC的两侧,设![]() .
.
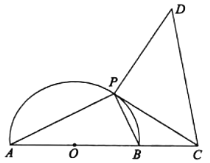
(1)把线段PC的长表示为![]() 的函数;
的函数;
(2)求四边形ACDP面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着食品安全问题逐渐引起人们的重视,有机、健康的高端绿色蔬菜越来越受到消费者的欢迎,同时生产—运输—销售一体化的直销供应模式,不仅减少了成本,而且减去了蔬菜的二次污染等问题.
(1)在有机蔬菜的种植过程中,有机肥料使用是必不可少的.根据统计某种有机蔬菜的产量与有机肥料的用量有关系,每个有机蔬菜大棚产量的增加量![]() (百斤)与使用堆沤肥料
(百斤)与使用堆沤肥料![]() (千克)之间对应数据如下表
(千克)之间对应数据如下表
使用堆沤肥料 | 2 | 4 | 5 | 6 | 8 |
产量的增加量 | 3 | 4 | 4 | 4 | 5 |
依据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并根据所求线性回归方程,估计如果每个有机蔬菜大棚使用堆沤肥料10千克,则每个有机蔬菜大棚产量增加量
;并根据所求线性回归方程,估计如果每个有机蔬菜大棚使用堆沤肥料10千克,则每个有机蔬菜大棚产量增加量![]() 是多少百斤?
是多少百斤?
(2)某大棚蔬菜种植基地将采摘的有机蔬菜以每份三斤称重并保鲜分装,以每份10元的价格销售到生鲜超市.“乐购”生鲜超市以每份15元的价格卖给顾客,如果当天前8小时卖不完,则超市通过促销以每份5元的价格卖给顾客(根据经验,当天能够把剩余的有机蔬菜都低价处理完毕,且处理完毕后,当天不再进货).该生鲜超市统计了100天有机蔬菜在每天的前8小时内的销售量(单位:份),制成如下表格(注:![]() ,且
,且![]() );
);
前8小时内的销售量(单位:份) | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
频数 | 10 | x | 16 | 6 | 15 | 13 | y |
若以100天记录的频率作为每日前8小时销售量发生的概率,该生鲜超市当天销售有机蔬菜利润的期望值为决策依据,当购进17份比购进18份的利润的期望值大时,求![]() 的取值范围.
的取值范围.
附:回归直线方程为![]() ,其中
,其中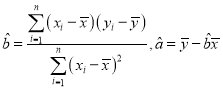 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com