
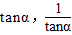 是关于x的方程
是关于x的方程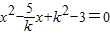 的两个实根,且
的两个实根,且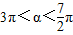 ,cosα+sinα= .
,cosα+sinα= . 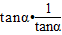 =k2-3=1,解之可得k值,由α所在象限可得tanα>0,进而可得
=k2-3=1,解之可得k值,由α所在象限可得tanα>0,进而可得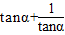 =
=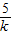 =
= ,化简可得tanα的方程,解之结合同角三角函数的基本关系可解得
,化简可得tanα的方程,解之结合同角三角函数的基本关系可解得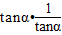 =k2-3=1,解得k=±2,
=k2-3=1,解得k=±2, π可推得2π+π<α<2π+
π可推得2π+π<α<2π+ π,
π,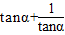 >0,∴
>0,∴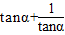 =
=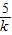 =
= ,
, ,
,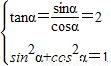 可解得sinα=
可解得sinα=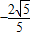 ,cosα=
,cosα=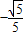 ,
, 时,由
时,由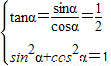 可解得sinα=
可解得sinα=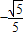 ,cosα=
,cosα=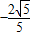 ,
,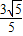 ,
,


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源:2012-2013学年山东省济宁市鱼台一中高三(上)期末数学模拟试卷(文科)(解析版) 题型:解答题
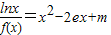 的根的个数.
的根的个数.查看答案和解析>>
科目:高中数学 来源:2010年浙江省杭州市高考最后冲刺数学试卷(理科)(解析版) 题型:解答题
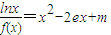 的根的个数.
的根的个数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com