思路:梯形中位线的定义是：连结梯形两腰中点的线段叫做梯形的中位线.这里要强调梯形中位线是连结两腰中点的线段，而不是连结两底中点的线段.梯形中位线定理的内容是:梯形中位线平行于两底，并且等于两底和的一半.该定理证明的关键是如何添加辅助线，把梯形中位线转化成三角形的中位线.
探究:设法把梯形中位线转化为三角形中位线.
图1-1-11
如图1-1-11，欲使MN成为某一个三角形的中位线，则梯形的一腰一定是三角形的一边，而三角形的另一边一定过梯形另一腰的中点.梯形的一个底应在三角形的第三边上，若连结AN并延长交BC的延长线于E(梯形的这种辅助线也经常用到)，就能得到这样的△ABE.这时只要证明AN=EN，AD=EC，问题就解决了.
关于梯形中位线与三角形中位线的一致性:
由梯形中位线公式MN=
(BC＋AD)，可知当AD退缩为一点时,其长度为零,则公式变为MN=
BC.这就是三角形的中位线公式,这体现了梯形中位线和三角形中位线的联系和一致性，反映了它们之间的辩证关系.
平行线等分线段定理的推论2“过梯形一腰的中点与底平行的直线必平分另一腰”，即梯形中位线.或说成“过梯形一腰的中点与底边平行的直线为梯形的中位线”，利用它可以判定某一线段为梯形中位线.
科目：高中数学 来源： 题型：
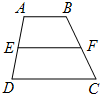（几何证明选讲选做题）如图，EF是梯形ABCD的中位线，记梯形ABFE的面积为S1，梯形CDEF的面积为S2，若| AB |
| CD |
| 1 |
| 2 |
| AB |
| EF |
| 2 |
| 3 |
| 2 |
| 3 |
| S1 |
| S2 |
| 5 |
| 7 |
| 5 |
| 7 |
查看答案和解析>>
科目：高中数学 来源：全优设计必修二数学苏教版 苏教版 题型：022
给出下列命题：
①矩形的平行投影一定是矩形；
②梯形的平行投影还是梯形；
③正方形的平行投影一定是菱形；
④平行四边形的平行投影可以是正方形；
⑤正投影一个平面图形时，投影的大小与原图形的大小一样；
⑥正三角形的平行投影可以是直角三角形；
⑦当三角形的平行投影仍为三角形时，则三角形的中位线还是投影三角形的中位线．
以上所有正确命题的序号为________．(要求把正确命题的序号都填上)并根据以上判断的结论归纳出平行投影的一些性质(越多越好)．
查看答案和解析>>
科目：高中数学 来源： 题型：
A.三角形的两边中点连线得到的中位线平行并且等于第三边的一半，类似地，三棱锥的中截面的面积等于底面面积的一半
B.三角形两边中点连线得到的中位线平行且等于第三边的一半，类似地，三棱锥的中截面的面积等于底面面积的
C.三角形被平行于一边的直线所截得的三角形与原三角形相似，面积比等于相似比的平方，类似地棱锥被平行于底面的平面所截得的多边形与底面相似，面积比等于相似比的平方
D.梯形的中位线等于两底和的一半，类似地，圆台的中截面半径等于上、下两底半径和的一半
查看答案和解析>>
科目：高中数学 来源：2014届湖南省高二4月段考数学理科试卷（解析版） 题型：选择题
在梯形ABCD中，AD//BC，对角线AC⊥BD，且AC=12，BD=9，则此梯形的
中位线长是（ ）．
A．
B．
C．
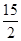D．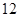
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
