若方程x2+(m+2)x+m+5=0只有正根,则m的取值范围是 .
【答案】
分析:根据一元二次方程与一元二次函数之间的关系可将二次方程x
2+(m+2)x+m+5=0只有正根转化为函数f(x)=x
2+(m+2)x+m+5与x轴的交点在x轴的正半轴上即
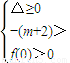
然后求出m的范围即可.
解答:解:∵方程x
2+(m+2)x+m+5=0只有正根
∴
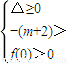
∴
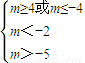
∴-5<m≤-4
故答案为-5<m≤-4
点评:本题主要考察了一元二次方程的根的分布.解题的关键是要熟知一元二次方程与一元二次函数之间的关系将根的问题转化为函数图象与x轴的交点问题即将对应的函数的图象根据题意固定然后再限制条件使图象满足题意也即“先定型,再定量”!

 轻松暑假总复习系列答案
轻松暑假总复习系列答案