练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于点D.

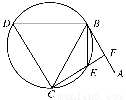
    (1)证明：DB＝DC；

    (2)设圆的半径为1，BC＝，延长CE交AB于点F，求△BCF外接圆的半径．

     

    （1）见解析（2）

    【解析】(1)证明：连接DE，交BC于点G.

    由弦切角定理，得∠ABE＝∠BCE，而∠ABE＝∠CBE，故∠CBE＝∠BCE，所以BE＝CE.

    又因为DB⊥BE，所以DE为圆的直径，∠DCE＝90°.

    由勾股定理可得DB＝DC.

    (2)由(1)知，∠CDE＝∠BDE，DB＝DC，

    故DG是BC边的中垂线，所以BG＝.

    设DE的中点为O，连接BO，则∠BOG＝60°，从而∠ABE＝∠BCE＝∠CBE＝30°，所以CF⊥BF，故Rt△BCF外接圆的半径等于

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学文复习二轮作业手册新课标·通用版限时集11讲练习卷（解析版） 题型：填空题

    如图所示，在四棱锥P－ABCD中，PA⊥底面ABCD，四边形ABCD为正方形，F为AB上一点．该四棱锥的正视图和侧视图如图所示，则四面体P－BFC的体积是________．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学文二轮专题复习与测试选修4-5不等式选讲 练习卷（解析版） 题型：填空题

    已知对于任意非零实数m，不等式|2m－1|＋|1－m|≥|m|(|x－1|－|2x＋3|)恒成立，则实数x的取值范围为____________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学文二轮专题复习与测试选修4-4坐标系与参数方程练习卷（解析版） 题型：填空题

    在平面直角坐标系xOy中，若直线l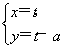： (t为参数)过椭圆C： (φ为参数)的右顶点，则常数a的值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学文二轮专题复习与测试选修4-1几何证明选讲练习卷（解析版） 题型：解答题

    如图，过圆O外一点P作该圆的两条割线PAB和PCD，分别交圆O于点A，B，C，D，弦AD和BC交于点Q，割线PEF经过点Q交圆O于点E，F，点M在EF上，且∠BAD＝∠BMF.

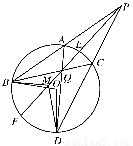
    (1)求证：PA·PB＝PM·PQ；

    (2)求证：∠BMD＝∠BOD.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学文二轮专题复习与测试解答题抢分训练练习卷（解析版） 题型：解答题

    在平面直角坐标系xOy中，O为坐标原点，A(－2,0)，B(2,0)，点P为动点，且直线AP与直线BP的斜率之积为－.

    (1)求动点P的轨迹C的方程；

    (2)过点D(1,0)的直线l交轨迹C于不同的两点M，N，△MON的面积是否存在最大值？若存在，求出△MON的面积的最大值及相应的直线方程；若不存在，请说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学文二轮专题复习与测试解答题保分训练练习卷（解析版） 题型：解答题

    已知数列{an}的相邻两项an，an＋1是关于x的方程x2－2nx＋bn＝0的两根，且a1＝1.

    (1)求证：数列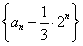是等比数列；

    (2)求数列{an}的前n项和Sn；

    (3)设函数f(n)＝bn－t·Sn(n∈N*)，若f(n)＞0对任意的n∈N*都成立，求t的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（四）第二章第一节练习卷（解析版） 题型：选择题

    函数f(x)=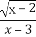+lg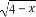的定义域是(　　)

    (A)(2,4) (B)(3,4)

    (C)(2,3)∪(3,4] (D)[2,3)∪(3,4)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（五）第二章第二节练习卷（解析版） 题型：填空题

    对a,b∈R,记max(a,b)=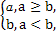函数f(x)=max(|x+1|,-x2+1)的最小值是　　　.

     

    查看答案和解析>>

    同步练习册答案