
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() ,
,![]() 轴上存在一点
轴上存在一点![]() 满足
满足![]() ,
,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 相切于第一象限上的点
相切于第一象限上的点![]() ,且分别与
,且分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由样本数据点集合![]() ,求得的回归直线方程为
,求得的回归直线方程为![]() ,且
,且![]() ,现发现两个数据点
,现发现两个数据点![]() 和
和![]() 误差较大,去除后重新求得的回归直线l的斜率为1.2,则( )
误差较大,去除后重新求得的回归直线l的斜率为1.2,则( )
A.变量x与y具有正相关关系B.去除后的回归方程为![]()
C.去除后y的估计值增加速度变快D.去除后相应于样本点![]() 的残差为0.05
的残差为0.05
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=etx(t>0),过点P(t,0)且平行于y轴的直线与曲线C:y=f(x)的交点为Q,曲线C过点Q的切线交x轴于点R,若S(1,f(1)),则△PRS的面积的最小值是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题. 该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取![]() 件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表 1是甲流水线样本的频数分布表,如图所示是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.表 1是甲流水线样本的频数分布表,如图所示是乙流水线样本的频率分布直方图.
表1 甲流水线样本的频数分布表
质量指标值 | 频数 |
|
|
|
|
|
|
|
|
|
|
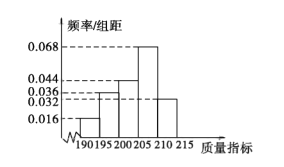
(1)若将频率视为概率,某个月内甲、乙两条流水线均生产了![]() 万件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
万件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(2)在甲流水线抽取的样本的不合格品中随机抽取两件,求两件不合格品的质量指标值均偏大的概率;
(3)根据已知条件完成下面![]() 列联表,并判断在犯错误概率不超过
列联表,并判断在犯错误概率不超过![]() 的前提下能否认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的前提下能否认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲生产线 | 乙生产线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() (其中
(其中![]() 为样本容量)
为样本容量)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第三届移动互联创新大赛,于2017年3月~10月期间举行,为了选出优秀选手,某高校先在计算机科学系选出一种子选手![]() ,再从全校征集出3位志愿者分别与
,再从全校征集出3位志愿者分别与![]() 进行一场技术对抗赛,根据以往经验,
进行一场技术对抗赛,根据以往经验, ![]() 与这三位志愿者进行比赛一场获胜的概率分别为
与这三位志愿者进行比赛一场获胜的概率分别为![]() ,且各场输赢互不影响.
,且各场输赢互不影响.
(1)求甲恰好获胜两场的概率;
(2)求甲获胜场数的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com