练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
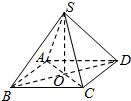
    16．如图，已知四棱锥S-ABCD的侧棱与底面边长都是2，且底面ABCD是正方形，则侧棱与底面所成的角（　　）
    A．75°B．60°C．45°D．30°

    分析 由条件利用正四棱锥的性质，利用直线和平面所成的角的定义找出侧棱与底面所成的角，再利用直角三角形中的边角关系，求得侧棱与底面所成的角．

    解答 解：由于四棱锥S-ABCD的侧棱与底面边长都是2，故四棱锥S-ABCD为正四棱锥，设O为底面正方形的中心，
    则∠SBO为侧棱与底面所成的角．
    直角三角形SBO中，cos∠SBO=$\frac{OB}{SB}$=$\frac{\sqrt{2}}{2}$，∴∠SBO=45°，
    故选：C．

    点评 本题主要考查正四棱锥的性质，直线和平面所成的角，直角三角形中的边角关系，体现了转化的数学思想，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    2．设函数f（x）=logax（a＞0，且a≠1）满足f（27）=3，则f-1（log92）的值是$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

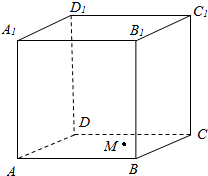    7．如图所示，正方体ABCD-A1B1C1D1的棱长为a，平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等，则点M的轨迹为（　　）
    A．直线B．椭圆C．抛物线D．双曲线

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．P到$（0，\sqrt{3}），（0，-\sqrt{3}）$距离之和为4，设点P的轨迹为C，直线y=kx+1与C交于AB
    （Ⅰ）求C的方程        
    （Ⅱ）若$\overrightarrow{OA}⊥\overrightarrow{OB}$，求k．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．设-1＜p＜1，f（x）=loga$\frac{1+2x}{1-2x}$+loga$\frac{1-2x}{2x-p}$（其中a＞0，且a≠1）
    （1）求f（x）的定义域；
    （2）求证：函数f（x）无零点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．cos24°cos36°-sin24°cos54°=（　　）
    A．cos12°B．sin12°C．$\frac{1}{2}$D．$-\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知函数f（x）的定义域是R，f′（x）是f（x）的导数，f（1）=e，g（x）=f′（x）-f（x），g（1）=0，g（x）的导数恒大于零，函数h（x）=f（x）-ex（e=2.71828…是自然对数的底数）的最小值是（　　）
    A．-1B．0C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．如图所示，已知正方体ABCD-A1B1C1D1，E、F分别是正方形A1B1C1D1和ADD1A1的中心，求EF和CD所成的角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．某化工厂生产一种化工产品，据负责该产品生产的部门预算，当该产品年产量在50吨至300吨之间时，其生产的总成本y（万元）与年产量x（吨）之间的部分对应数据大致如下表：
    生产量x（单位：吨）50100130180200250300
    生产总成本y（单位：万元）2750200017501800205027504050
    （1）给出如下四个函数：
    ①y=ax2+b，②y=$\frac{1}{10}{x}^{2}+ax+b$，③y=a•bx，④y=a•logbx．根据上表数据，从上述四个函数中选取一个最恰当的函数描述y与x的变化关系，并通过表中前两组数据，求出y与x的函数解析式；
    （2）根据你求出的函数解析式，试问当年产量为多少吨时，生产每吨的平均成本最低？每吨的最低成本是多少？
    （3）若将每吨产品的出厂价定为16万元，则年产量为多少吨时，方可使得全年的利润最大？并求出全年的最大利润．

    查看答案和解析>>

    同步练习册答案