练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （文）设x∈R，[x]表示不大于x的最大整数，如：[π]=3，[-1.2]=-2，[0.5]=0，则使[x2-1]=3的x的取值范围是（　　）
    分析：根据[x]的取值意义，由[x2-1]=3得到3≤x2-1＜4然后解不等式即可．
    解答：解：根据定义可知，若[x2-1]=3，则3≤x2-1＜4即4≤x2＜5，
    所以解得2≤x＜
    		5
    或-
    		5
    ＜x≤-2    ．
    故x的取值范围是（-
    		5
    ，-2]∪[2，
    		5
    ）．
    故选C．
    点评：本题主要考查对新定义的理解和应用，由[x2-1]=3得到3≤x2-1＜4是解决本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    规定，其中，m是正整数，且，这是组合数（n、m是正整数，且m≤n）的一种推广．

    （1）求的值；

    （2）（文）设x＞0．当x为何值时，取得最小值?

    　　（理）组合数的两个性质：

    　　 ①    ②

    是否都能推广到（x∈R，m是正整数）的情形?

    若能推广，则写出推广的形式并给出证明；若不能，则说明理由．

    （3）（文）同（理）（2）

    　　（理）已知组合数是正整数，证明：当x∈Z，m是正整数时，∈Z．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    （文）设x∈R，[x]表示不大于x的最大整数，如：[π]=3，[-1.2]=-2，[0.5]=0，则使[x2-1]=3的x的取值范围是


    1. A.
      [2，数学公式）
    2. B.
      （-数学公式，-2]
    3. C.
      （-数学公式，-2]∪[2，数学公式）
    4. D.
      [-数学公式，-2]∪[2，数学公式]

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建省福州外国语学校高二（上）期中数学试卷（解析版） 题型：选择题

    （文）设x∈R，[x]表示不大于x的最大整数，如：[π]=3，[-1.2]=-2，[0.5]=0，则使[x2-1]=3的x的取值范围是（ ）
    A．[2，）
    B．（-，-2]
    C．（-，-2]∪[2，）
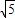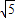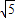    D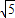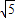．[-，-2]∪[2，]

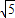    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年长郡中学一模文）设{x}表示离x最近的整数，即若≤(m∈Z)，则{x} = m．给出下列关于函数的四个命题：
    ①函数的定义域是R，值域是[0，]；
    ②函数的图像关于直线(k∈Z)对称；
    ③函数是周期函数，最小正周期是1；
    ④函数在上是增函数．
    其中真命题的个数是（     ）．

    A．1                          B．2                          C．3                       D．4

    查看答案和解析>>

    同步练习册答案