
分析 先由极坐标方程求出直角坐标方程,然后转化为参数方程吗,利用参数的应用建立方程组进行求解即可.
解答 解:由直线l的极坐标方程是$ρsin(θ-\frac{π}{6})=\frac{3}{2}$,可得由直线l的直角坐标方程是$\sqrt{3}y-x=3$,
化为参数方程为$\left\{\begin{array}{l}x=-3+\frac{{\sqrt{3}}}{2}s\\ y=\frac{s}{2}\end{array}\right.$(s为参数);曲线$C:\left\{\begin{array}{l}x=t+\frac{1}{t}\\ y=t-\frac{1}{t}\end{array}\right.$(t为参数)可化为x2-y2=4.
将直线的参数方程代入x2-y2=4,得${s^2}-6\sqrt{3}s+10=0$.
设A,B所对应的参数为s1,s2,${s_1}+{s_2}=6\sqrt{3}$,s1s2=10,
所以$|{AB}|=\sqrt{{{({s_1}+{s_2})}^2}-4{s_1}{s_2}}=2\sqrt{17}$.
点评 本题主要考查坐标系和参数方程的应用,根据极坐标和参数方程进行转化是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{4}$) | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,1) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{12}$+kπ,$\frac{5π}{12}$+kπ](k∈Z) | B. | [-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z) | ||
| C. | [-$\frac{2π}{3}$+4kπ,$\frac{4π}{3}$+4kπ](k∈Z) | D. | [-$\frac{5π}{6}$+4kπ,$\frac{7π}{6}$+4kπ](k∈Z) |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:填空题
若集合 满足
满足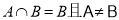 ,则命题“
,则命题“ ”是命题“
”是命题“ ”的 条件.(填“充分不必要”,“必要不充分”,“充要”)
”的 条件.(填“充分不必要”,“必要不充分”,“充要”)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,$\frac{3}{2}$) | C. | ($\frac{1}{2}$,$\frac{5}{2}$) | D. | ($\frac{3}{2}$,$\frac{5}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,CC1=2,点P是侧棱C1C的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,CC1=2,点P是侧棱C1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a3>b3 | B. | $\frac{1}{a}$<$\frac{1}{b}$ | C. | lga>lgb | D. | $\sqrt{a}$>$\sqrt{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{{6\sqrt{13}}}{13}$ | C. | $\frac{{4\sqrt{13}}}{13}$ | D. | $\frac{{2\sqrt{13}}}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com