
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,经过点
,经过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
科目:高中数学 来源: 题型:
【题目】已知A是抛物线E:y2=2px(p>0)上的一点,以点A和点B(2,0)为直径两端点的圆C交直线x=1于M,N两点.
(1)若|MN|=2,求抛物线E的方程;
(2)若0<p<1,抛物线E与圆(x﹣5)2+y2=9在x轴上方的交点为P,Q,点G为PQ的中点,O为坐标原点,求直线OG斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉,字谦光,南宋时期杭州人.在他1261年所著的《详解九章算法》一书中,辑录了如图所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪中叶(约公元1050年)贾宪的《释锁算术》,并绘画了“古法七乘方图”.故此,杨辉三角又被称为“贾宪三角”.杨辉三角是一个由数字排列成的三角形数表,一般形式如下:
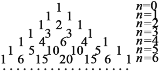
基于上述规律,可以推测,当![]() 时,从左往右第22个数为_____________.
时,从左往右第22个数为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各射击一次,击中目标的概率分别是![]() 和
和![]() ,假设两人射击是否击中目标相互没有影响,每人每次射击是否击中目标相互也没有影响.
,假设两人射击是否击中目标相互没有影响,每人每次射击是否击中目标相互也没有影响.
(1)求甲、乙两人各射击一次均击中目标的概率;
(2)若乙在射击中出现连续![]() 次未击中目标则会被终止射击,求乙恰好射击
次未击中目标则会被终止射击,求乙恰好射击![]() 次后被终止射击的概率.
次后被终止射击的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,侧面
是正方形,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点,
中点,![]() .
.

(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市教育与环保部门联合组织该市中学参加市中学生环保知识团体竞赛,根据比赛规则,某中学选拔出8名同学组成参赛队,其中初中学部选出的3名同学有2名女生;高中学部选出的5名同学有3名女生,竞赛组委会将从这8名同学中随机选出4人参加比赛.
(Ⅰ)设“选出的4人中恰有2名女生,而且这2名女生来自同一个学部”为事件![]() ,求事件
,求事件![]() 的概率
的概率![]() ;
;
(Ⅱ)设![]() 为选出的4人中女生的人数,求随机变量
为选出的4人中女生的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在A,B实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在A,B试验地随机抽选各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80及以上的花苗为优质花苗.

(1)求图中a的值,并求综合评分的中位数;
(2)用样本估计总体,以频率作为概率,若在A,B两块实验地随机抽取3棵花苗,求所抽取的花苗中的优质花苗数的分布列和数学期望;
(3)填写下面的列联表,并判断是否有90%的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P—ABC中,PA⊥平面ABC,AC⊥BC,D为PC中点,E为AD中点,PA=AC=2,BC=1.

(1)求证:AD⊥平面PBC:
(2)求PE与平面ABD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中为了了解高三学生每天自主参加体育锻炼的情况,随机抽取了100名学生进行调查,其中女生有55名.下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图:

将每天自主参加体育锻炼时间不低于40分钟的学生称为体育健康![]() 类学生,已知体育健康
类学生,已知体育健康![]() 类学生中有10名女生.
类学生中有10名女生.
(1)根据已知条件完成下面![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为达到体育健康
的把握认为达到体育健康![]() 类学生与性别有关?
类学生与性别有关?
非体育健康 | 体育健康 | 合计 | |
男生 | |||
女生 | |||
合计 |
(2)将每天自主参加体育锻炼时间不低于50分钟的学生称为体育健康![]() 类学生,已知体育健康
类学生,已知体育健康![]() 类学生中有2名女生,若从体育健康
类学生中有2名女生,若从体育健康![]() 类学生中任意选取2人,求至少有1名女生的概率.
类学生中任意选取2人,求至少有1名女生的概率.
附:
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com