
【题目】以![]() 为直径的圆上每一点都染上了红、黄、蓝三色之一,已知
为直径的圆上每一点都染上了红、黄、蓝三色之一,已知![]() 、
、![]() 染上了红色,联结圆上的点组成三角形,给出4个结论:
染上了红色,联结圆上的点组成三角形,给出4个结论:
①必定存在一个直角三角形,三个顶点同为红色;
②必定存在一个直角三角形,三个顶点同色;
③必定存在一个直角三角形,三个顶点全不同色;
④必定存在一个直角三角形,或都三个顶点同色,或者三个顶点全不同色。
则真命题的个数是( )个。
A. 1 B. 2
C. 3 D. 4
【答案】A
【解析】
易知,联结圆上的点组成直角三角形,当且仅当斜边为直径,下面讨论直径.若除点![]() 、
、![]() 外,圆上再无红点,则结论①不成立;若除点
外,圆上再无红点,则结论①不成立;若除点![]() 、
、![]() 外,圆上再无红点,且其他所有直径的两端点都黄、蓝异色,则结论②不成立;若圆上所有直径的两端点都同色,则结论③不成立.下面证明:结论④成立.若除点
外,圆上再无红点,且其他所有直径的两端点都黄、蓝异色,则结论②不成立;若圆上所有直径的两端点都同色,则结论③不成立.下面证明:结论④成立.若除点![]() 、
、![]() 外,圆上还有红点,则存在三个顶点同色的直角三角形(同红色),命题成立,若除点
外,圆上还有红点,则存在三个顶点同色的直角三角形(同红色),命题成立,若除点![]() 、
、![]() 外,圆上再无红点(即圆上其余点染上了黄、蓝两色之一),则作直径
外,圆上再无红点(即圆上其余点染上了黄、蓝两色之一),则作直径![]() ,当
,当![]() 两端异色时,存在三个顶点全不同色的直角三角形,命题成立;当
两端异色时,存在三个顶点全不同色的直角三角形,命题成立;当![]() 两端同色时,不妨记为同黄色,若此时圆上还有第三个黄点,则存在三个顶点同黄色的直角三角形,命题成立.若此时圆上没有第三个黄点,即除点
两端同色时,不妨记为同黄色,若此时圆上还有第三个黄点,则存在三个顶点同黄色的直角三角形,命题成立.若此时圆上没有第三个黄点,即除点![]() 、
、![]() 、
、![]() 、
、![]() 外圆上全为蓝点,则存在三个顶点同蓝色的直角三角形,命题成立。综上得结论④成立。
外圆上全为蓝点,则存在三个顶点同蓝色的直角三角形,命题成立。综上得结论④成立。


科目:高中数学 来源: 题型:
【题目】某次数学测验共有12道选择题,每道题共有四个选项,且其中只有一个选项是正确的,评分标准规定:每选对1道题得5分,不选或选错得0分. 在这次数学测验中,考生甲每道选择题都按照规则作答,并能确定其中有9道题能选对;其余3道题无法确定正确选项,在这3道题中,恰有2道能排除两个错误选项,另1题只能排除一个错误选项. 若考生甲做这3道题时,每道题都从不能排除的选项中随机挑选一个选项作答,且各题作答互不影响.在本次测验中,考生甲选择题所得的分数记为![]()
(1)求![]() 的概率;
的概率;
(2)求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有6人参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择,为增加趣味性,主办方制作了一款电脑软件:按下电脑键盘“![]() ”键则会出现模拟抛两枚质地均匀的骰子的画面,若干秒后在屏幕上出现两个点数
”键则会出现模拟抛两枚质地均匀的骰子的画面,若干秒后在屏幕上出现两个点数![]() 和
和![]() ,并在屏幕的下方计算出
,并在屏幕的下方计算出![]() 的值.主办方现规定:每个人去按“
的值.主办方现规定:每个人去按“![]() ”键,当显示出来的
”键,当显示出来的![]() 小于
小于![]() 时则参加甲游戏,否则参加乙游戏.
时则参加甲游戏,否则参加乙游戏.
(1)求这6个人中恰有2人参加甲游戏的概率;
(2)用![]() 、
、![]() 分别表示这6个人中去参加甲,乙游戏的人数,记
分别表示这6个人中去参加甲,乙游戏的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的右顶点
的右顶点![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知![]() (异于点
(异于点![]() )为椭圆
)为椭圆![]() 上一个动点,过
上一个动点,过![]() 作线段
作线段![]() 的垂线
的垂线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO=![]() .
.

(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的周长为
的周长为![]() ,
, ![]() 的离心率
的离心率![]()
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 的交点是否恒在一条定直线上?若是,求该定直线的方程;否则,说明理由.
的交点是否恒在一条定直线上?若是,求该定直线的方程;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查观众对电影“复仇者联盟4”结局的满意程度,研究人员在某电影院随机抽取了1000名观众作调查,所得结果如下所示,其中不喜欢“复仇者联盟4”的结局的观众占被调查观众总数的![]() .
.
男性观众 | 女性观众 | 总计 | |
喜欢“复仇者联盟4”的结局 | 400 | ||
不喜欢“复仇者联盟4”的结局 | 200 | ||
总计 |
(Ⅰ)完善上述![]() 列联表;
列联表;
(Ⅱ)是否有99.9%的把握认为观众对电影“复仇者联盟4”结局的满意程度与性别具有相关性?
附: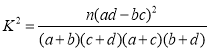
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com